
题目列表(包括答案和解析)
20. (本小题满分13分)
设数列 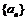 的前项和为
的前项和为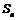 ,且
,且 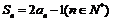 .
.
(I)求数列 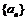 的通项公式;
的通项公式;
(Ⅱ)设数列 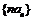 的前n项和为
的前n项和为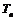 ,对任意
,对任意 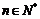 ,比较
,比较 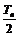 与
与  的大小.
的大小.
19.(Ⅰ)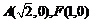 .椭圆
.椭圆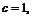
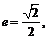 ,
,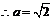 ,
,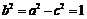 ,
,
 .
………………5分
.
………………5分
(Ⅱ)设点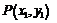 ,过点的圆的切线方程为
,过点的圆的切线方程为 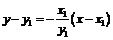 即
即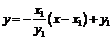 。
。
由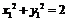 得
得 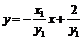 ,令
,令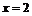 得
得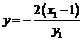 ,故点
,故点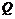
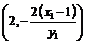
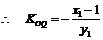 ,又
,又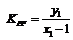
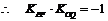
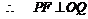 .
………………………………12分
.
………………………………12分
19.(本小题满分12分)
已知圆 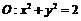 交轴正半轴于点A,点F满足
交轴正半轴于点A,点F满足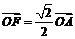 ,以F为右焦点的椭圆的离心率为
,以F为右焦点的椭圆的离心率为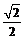 .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设过圆上一点P的切线交直线
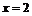 于点Q,求证:
于点Q,求证: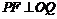 .
.
1.巢湖市二模
17. 有一座大桥既是交通拥挤地段,又是事故多发地段,为了保证安全,交通部门规定。大桥上的车距d(m)与车速v(km/h)和车长l(m)的关系满足: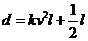 (k为正的常数),假定车身长为4m,当车速为60(km/h)时,车距为2.66个车身长。
(k为正的常数),假定车身长为4m,当车速为60(km/h)时,车距为2.66个车身长。
(1)写出车距d关于车速v的函数关系式;
(2)应规定怎样的车速,才能使大桥上每小时通过的车辆最多?
18, 抛物线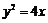 的焦点为F,
的焦点为F,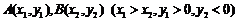 在抛物线上,且存在实数λ,使
在抛物线上,且存在实数λ,使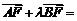 0,
0,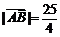 .
.
(1)求直线AB的方程;
(2)求△AOB的外接圆的方程.
19, 设函数 。
。
(Ⅰ)求 的单调区间和极值;
的单调区间和极值;
(Ⅱ)若对一切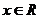 ,
,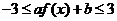 ,求
,求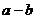 的最大值。
的最大值。
20, 设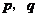 为实数,
为实数,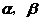 是方程
是方程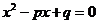 的两个实根,数列
的两个实根,数列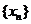 满足
满足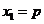 ,
,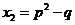 ,
,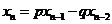 (
( …).
…).
(1)证明: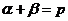 ,
,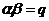 ;
;
(2)求数列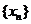 的通项公式;
的通项公式;
(3)若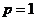 ,
,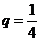 ,求
,求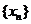 的前
的前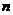 项和
项和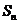 .
.
14. 下列说法:①当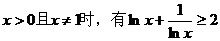 ;②
;②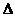 ABC中,
ABC中,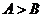 是
是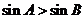 成立的充要条件;③函数
成立的充要条件;③函数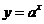 的图象可以由函数
的图象可以由函数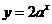 (其中
(其中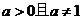 )平移得到;④已知
)平移得到;④已知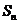 是等差数列
是等差数列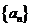 的前
的前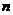 项和,若
项和,若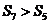 ,则
,则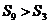 .;⑤函数
.;⑤函数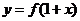 与函数
与函数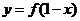 的图象关于直线
的图象关于直线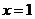 对称。其中正确的命题的序号为
。
对称。其中正确的命题的序号为
。
二:解答题:
15, 已知函数f(x)=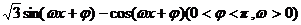 为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为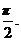
(Ⅰ)求f(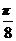 )的值;
)的值;
(Ⅱ)将函数y=f(x)的图象向右平移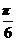 个单位后,再将得到的图象上各点的横坐标舒畅长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标舒畅长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
16, 如图,在多面体ABCDE中,AE⊥ABC,BD∥AE,
且AC=AB=BC=BD=2,AE=1,F在CD上(不含C, D两点)
(1)求多面体ABCDE的体积;
(2)若F为CD中点,求证:EF⊥面BCD;
 (3)当
(3)当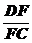 的值=
时,能使AC ∥平面EFB,并给出证明。
的值=
时,能使AC ∥平面EFB,并给出证明。
13. 设O是△ABC内部一点,且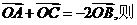
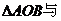
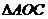 的面积之比为
的面积之比为
.
12. 设方程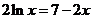 的解为
的解为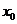 ,则关于
,则关于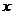 的不等式
的不等式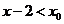 的最大整数解为
的最大整数解为
11. 过椭圆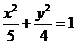 的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,则△OAB的面积为______________
的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,则△OAB的面积为______________
10. 电子钟一天显示的时间是从00:00到23:59的每一时刻都由四个数字组成,则一天中任一时刻的四个数字之和为23的概率为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com