
题目列表(包括答案和解析)
21.(本题满分12分)解: (Ⅰ)∵椭圆E: 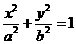 (a,b>0)经过M(-2,
(a,b>0)经过M(-2,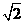 ) ,一个焦点坐标为
) ,一个焦点坐标为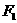 (
(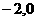 ),∴
),∴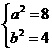 ,椭圆E的方程为
,椭圆E的方程为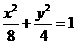 ; …………………4分
; …………………4分
(Ⅱ)当直线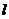 的斜率存在时,设直线
的斜率存在时,设直线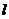 与椭圆E的两个交点为A(
与椭圆E的两个交点为A(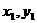 ),B(
),B(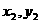 ),相交所得弦的中点
),相交所得弦的中点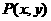 ,∴
,∴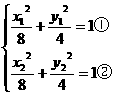 ,
,
①-②得,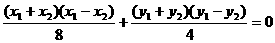 ,
,
∴弦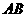 的斜率
的斜率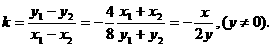 ,
,
∵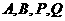 四点共线,∴
四点共线,∴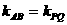 ,即
,即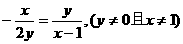 ,
,
经检验(0,0),(1,0)符合条件,
∴线段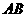 中点
中点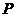 的轨迹方程是
的轨迹方程是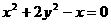 .…………………8分
.…………………8分
(Ⅲ)当⊙ 的切线斜率存在时,设⊙
的切线斜率存在时,设⊙ 的切线方程为
的切线方程为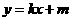 ,
,
由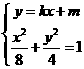 得
得 ,设
,设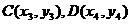 ,则
,则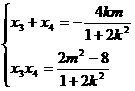 ∵
∵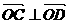 ,∴
,∴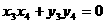 ,即
,即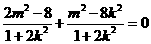 ,
,
∴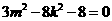 ,即
,即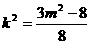 ,∵直线
,∵直线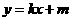 为⊙
为⊙ 的一条切线,
的一条切线,
∴圆的半径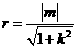 , 即
, 即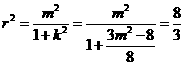 ,
,
经检验,当⊙ 的切线斜率不存在时也成立.∴
的切线斜率不存在时也成立.∴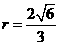 .…………12分
.…………12分
21. (本题满分12分)
已知椭圆E: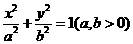 的焦点坐标为
的焦点坐标为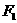 (
(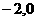 ),点M(
),点M(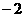 ,
,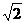 )在椭圆E上.
)在椭圆E上.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设Q(1,0),过Q点引直线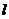 与椭圆E交于
与椭圆E交于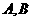 两点,求线段
两点,求线段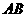 中点
中点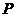 的轨迹方程;(Ⅲ)O为坐标原点,⊙
的轨迹方程;(Ⅲ)O为坐标原点,⊙ 的任意一条切线与椭圆E有两个交点
的任意一条切线与椭圆E有两个交点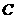 ,
,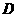 且
且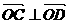 ,求⊙
,求⊙ 的半径.
的半径.
20. (Ⅰ)由题意知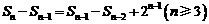 即
即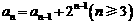
∴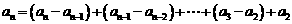
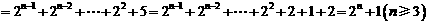
检验知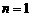 、
、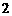 时,结论也成立,故
时,结论也成立,故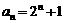 .
.
(Ⅱ)由于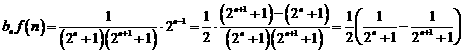
故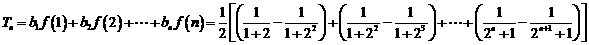
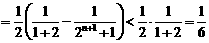 .
.
20. (本题满分12分)
已知数列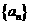 中,
中,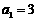 ,
,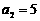 ,其前
,其前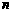 项和
项和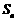 满足
满足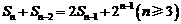 .令
.令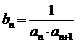 .
.
(Ⅰ)求数列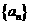 的通项公式;
的通项公式;
(Ⅱ)若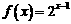 ,求证:
,求证: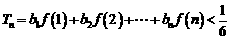 (
(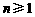 ).
).
1. 河南一模
22.(本小题满分16分)
解:(1)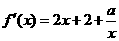
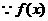 在(0,1)上单调
在(0,1)上单调
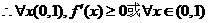
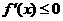 (这是城“=”只对个别
(这是城“=”只对个别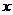 成立)
成立)
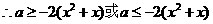
从而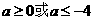 7分
7分
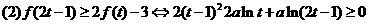 ①
①
令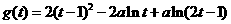
则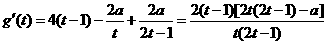
当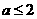 时
时
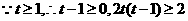
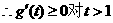 恒成立,
恒成立,
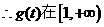 上递增,
上递增,
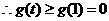 ,即1式对
,即1式对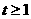 恒成立。
恒成立。
当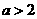 时,
时,
令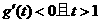 ,
,
解得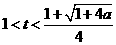
于是,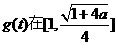 上递减,在
上递减,在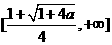 上递增,
上递增,
从而有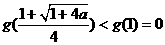 ,即①式不可能恒成立。
,即①式不可能恒成立。
综上所述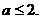 16分
16分
22.(本小题满分16分)
已知函数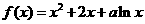
(1)若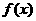 是区间(0,1)上单调函数,求
是区间(0,1)上单调函数,求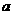 的取值范围;
的取值范围;
(2)若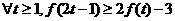 ,试求
,试求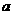
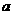 的取值范围。
的取值范围。
21.(本小题满分14分)
解:(1)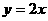 ,
,
设切点分别为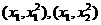
则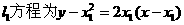
即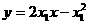 ①
①
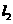 方程为
方程为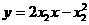 ②
②
由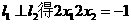
即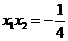
所以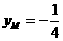 ,即点M的纵坐标为定值
,即点M的纵坐标为定值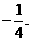
(2)设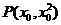 ,
,
则C1在点P处切线方程为: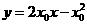
代入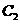 方程
方程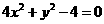
得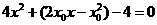
即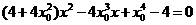
设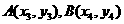
则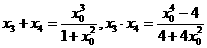
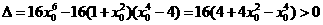 ③
③
由(1)知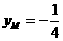
从而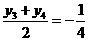 ,
,
即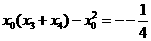
进而得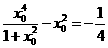
解得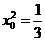 ,且满足③
,且满足③
所以这样点P存在,其坐标为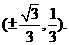 14分
14分
21.(本小题满分14分)
已知抛物线
(1)设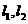 是C1的任意两条互相垂直的切线,并设
是C1的任意两条互相垂直的切线,并设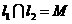 ,证明:点M的纵坐标为定值;
,证明:点M的纵坐标为定值;
(2)在C1上是否存在点P,使得C1在点P处切线与C2相交于两点A、B,且AB的中垂线恰为C1的切线?若存在,求出点P的坐标;若不存在,说明理由。
22.(1)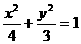 ;
;
(2)m=3, 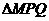 面积的最大值是
面积的最大值是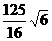
权所有:()
3浙江十校模一
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com