
题目列表(包括答案和解析)
5.已知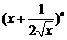 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.
(Ⅰ)求n的值;(Ⅱ)求展开式中系数最大的项.
4.已知函数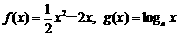 (a>0,且a≠1),其中为常数.如果
(a>0,且a≠1),其中为常数.如果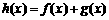 是增函数,且
是增函数,且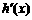 存在零点(
存在零点(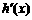 为
为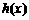 的导函数).(Ⅰ)求a的值;
的导函数).(Ⅰ)求a的值;
(Ⅱ)设A(x1,y1)、B(x2,y2)(x1<x2)是函数y=g(x)的图象上两点,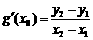 (
(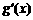 为
为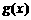 的导函数),证明:
的导函数),证明: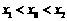 .
.
3.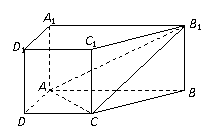 直棱柱
直棱柱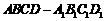 中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,
中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,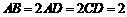 .(Ⅰ)求证:AC⊥平面BB1C1C;(Ⅱ)在A1B1上是否存一点P,使得DP与平面BCB1与平面ACB1都平行?证明你的结论.
.(Ⅰ)求证:AC⊥平面BB1C1C;(Ⅱ)在A1B1上是否存一点P,使得DP与平面BCB1与平面ACB1都平行?证明你的结论.
1.在△ABC中,角A,B,C所对边分别为a,b,c,且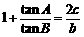 .
.
(Ⅰ)求角A;(Ⅱ)若m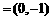 ,n
,n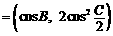 ,试求|m
,试求|m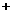 n|的最小值.
n|的最小值.
 2
2 口袋中有质地、大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.(Ⅰ)求甲赢且编号的和为6的事件发生的概率;
口袋中有质地、大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.(Ⅰ)求甲赢且编号的和为6的事件发生的概率;
(Ⅱ)这种游戏规则公平吗?试说明理由.
16.已知数列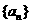 满足
满足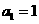 ,且
,且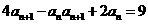 (
(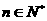 )
)
(1)求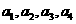 的值;(2)由(1)猜想
的值;(2)由(1)猜想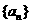 的通项公式,并给出证明.
的通项公式,并给出证明.
15.某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(是不小于40不大于100的整数)分成六段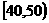 ,
,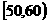 …
…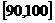 后
后
(1)求第四小组的频率,并补全这个画出如下部分频率分布直方图.
 (2) 观察频率分布直方图图形的 信息,估计这次考试的及格率(60分及以上为及格)和平均分.
(2) 观察频率分布直方图图形的 信息,估计这次考试的及格率(60分及以上为及格)和平均分.
14.已知点P是抛物线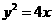 上的动点,点P在y轴上的射影是M,点A的坐标是(4,a),则当
上的动点,点P在y轴上的射影是M,点A的坐标是(4,a),则当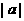
 4时,
4时,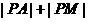 的最小值是
.
的最小值是
.
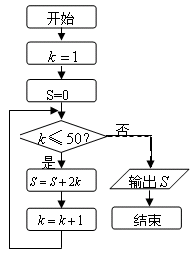
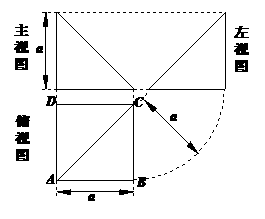
13.四棱锥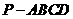 的顶点P在底面ABCD中的投影恰好是A,其三视图如图:
的顶点P在底面ABCD中的投影恰好是A,其三视图如图:
则四棱锥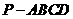 的表面积为 .
的表面积为 .
12.函数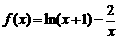 的零点所在的区间是(n,n+1),则正整数n=______.
的零点所在的区间是(n,n+1),则正整数n=______.
11.已知数列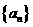 为等差数列,且
为等差数列,且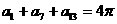 ,则
,则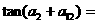 ________.
________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com