
题目列表(包括答案和解析)
21.已知:函数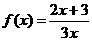 ,数列
,数列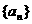 对
对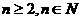 总有
总有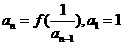 ;
;
(1)求{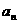 }的通项公式。(2) 求和:
}的通项公式。(2) 求和: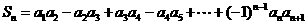
(3)若数列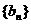 满足:①
满足:①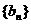 为
为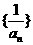 的子数列(即
的子数列(即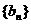 中的每一项都是
中的每一项都是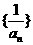 的项,且按在
的项,且按在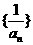 中的顺序排列)②
中的顺序排列)②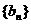 为无穷等比数列,它的各项和为
为无穷等比数列,它的各项和为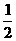 。这样的数列是否存在?若存在,求出所有符合条件的数列
。这样的数列是否存在?若存在,求出所有符合条件的数列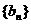 ,写出它的通项公式,并证明你的结论;若不存在,说明理由。
,写出它的通项公式,并证明你的结论;若不存在,说明理由。
解(1)由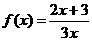 ,又
,又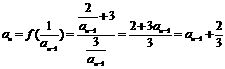
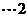 分
分
所以,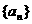 是以
是以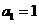 为首项,
为首项,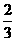 为公差的等差数列,即
为公差的等差数列,即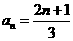

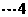 分
分
(2)当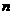 为偶数,
为偶数,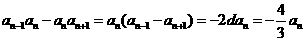
所以 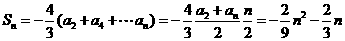
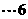 分
分
当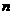 为奇数,则
为奇数,则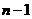 为偶数,
为偶数,
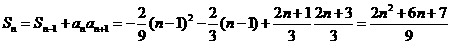
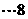 分
分
综上: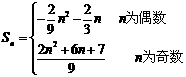
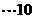 分
分
(3)设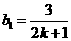 ,公比
,公比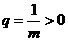 ,则
,则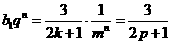 (
(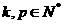 )对任意的
)对任意的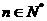 均成立,故
均成立,故 是正奇数,又
是正奇数,又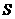 存在,所以
存在,所以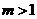
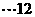 分
分
当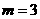 时,
时,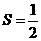 ,此时
,此时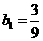 ,
,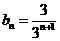 ,成立
,成立
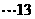 分
分
当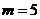 时,
时,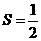 ,此时
,此时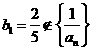 故不成立
故不成立
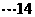 分
分
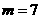 时,
时,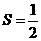 ,此时
,此时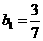 ,
,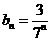 ,成立
,成立
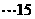 分
分
当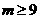 时,
时,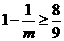 ,由
,由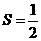 ,得
,得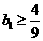 ,设
,设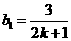 ,则
,则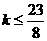 ,又因为
,又因为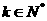 ,所以
,所以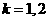 ,此时
,此时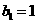 或
或 分别代入
分别代入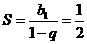 ,得到
,得到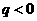 不合题意
不合题意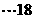 分
分
由此,满足条件(3)的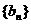 只有两个,即
只有两个,即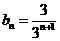 或
或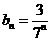
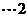 0分
0分
20.已知函数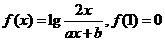 ,当
,当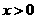 时,恒有
时,恒有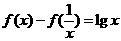
(1)求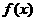 的表达式;
的表达式;
(2)设不等式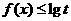 的解集为A,且
的解集为A,且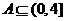 ,求实数
,求实数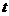 的取值范围。
的取值范围。
(3)若方程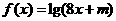 的解集为
的解集为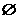 ,求实数
,求实数 的取值范围。
的取值范围。
解:(1) 当
当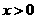 时,
时,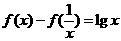 恒成立
恒成立
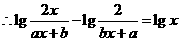 ,即
,即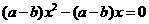 恒成立,
恒成立,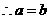
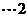 分
分
又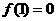 ,即
,即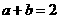 ,从而
,从而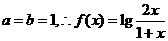
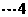 分
分
(2)由不等式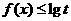 ,
,
即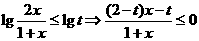 且
且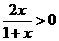
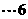 分
分
由于解集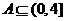 ,故
,故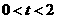 ,
,
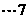 分
分
所以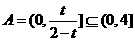 即
即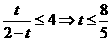 ,
, 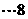 分
分
又因为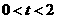 ,所以实数
,所以实数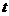 的取值范围是
的取值范围是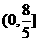
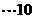 分
分
(3)解法一:
由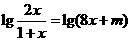
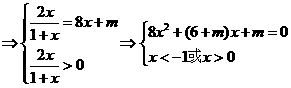
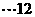 分
分
方程的解集为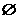 ,故有两种情况:
,故有两种情况:
①方程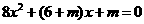 无解,即
无解,即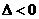 ,得
,得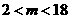
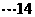 分
分
②方程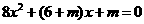 有解,两根均在
有解,两根均在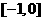 内,
内,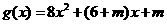
则
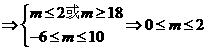
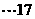 分
分
综合①②得实数 的取值范围是
的取值范围是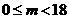
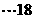 分
分
(3)解法二:
若方程有解,
则由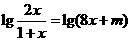
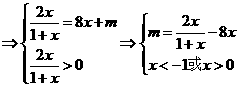
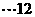 分
分
由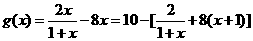
当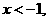 则
则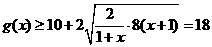 ,
,
当且仅当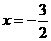 时取到18
时取到18
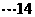 分
分
当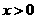 ,则
,则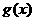 是减函数,所以
是减函数,所以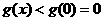
即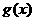 在
在 上的值域为
上的值域为
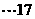 分
分
故当方程无解时, 的取值范围是
的取值范围是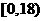
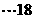 分
分
19.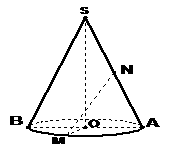 已知圆锥的底面半径
已知圆锥的底面半径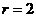 ,半径
,半径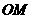 与母线
与母线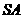 垂直,
垂直,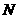 是
是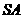 中点,
中点,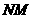 与高
与高 所成的角为
所成的角为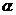 ,且
,且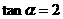
(理)(1)求圆锥的体积;(2)求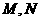 两点在圆锥侧面上的最短距离。
两点在圆锥侧面上的最短距离。
(文)(1)证明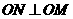 ;(2)求圆锥的体积。
;(2)求圆锥的体积。
解 (1)设 中点
中点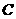 ,连接NC、CM,则
,连接NC、CM,则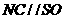 ,
,
故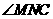 即为
即为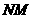 与高
与高 所成的角
所成的角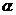 ,
, 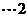 分
分
又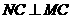 且
且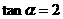 所以
所以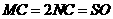 ,
,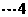 分
分
又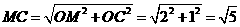 ,即
,即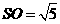 ,
,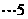 分
分
从而圆锥的体积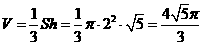
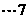 分
分
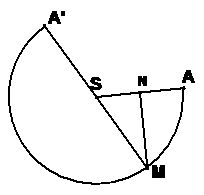 (2)作圆锥的侧面展开图,线段MN即为所求最短距离。
(2)作圆锥的侧面展开图,线段MN即为所求最短距离。 分
分
由已知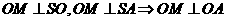 ,
,
故M是弧AB的中点,即M是扇形弧的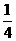 点。
点。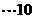 分
分
因为扇形弧长即为圆锥底面周长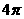 ,
,
由(1)知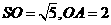 ,所以母线
,所以母线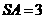 ,
,
从而扇形的中心角为 ,所以
,所以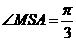
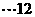 分
分
在三角形MSA中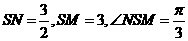 ,由余弦定理得
,由余弦定理得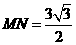
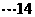 分
分
18.已知函数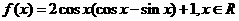
(1)求函数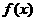 的最小正周期;
的最小正周期;
(2)求函数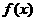 在区间
在区间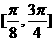 上的最小值与最大值。
上的最小值与最大值。
(3)(理)将函数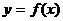 的图像按向量
的图像按向量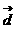 平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的
平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的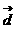
(文)将函数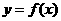 的图像沿
的图像沿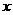 轴正方向平移
轴正方向平移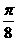 个单位,再沿
个单位,再沿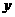 轴负方向平移2个单位得到
轴负方向平移2个单位得到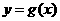 的图象,求
的图象,求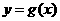 的解析式。
的解析式。
解(1)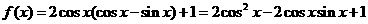

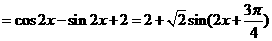
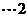 分
分
因此,函数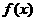 的最小正周期为
的最小正周期为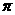
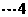 分
分
(2)因为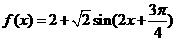 在区间
在区间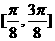 上是减函数,在区间
上是减函数,在区间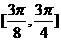 上是增函数,又
上是增函数,又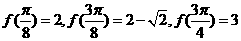
 分
分
所以,函数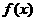 在区间
在区间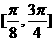 上的最大值为
上的最大值为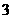 ,最小值为
,最小值为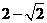
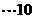 分
分
(3)设平移后的图像的函数解析式为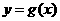 ,因为
,因为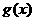 的图像关于原点成中心对称,所以
的图像关于原点成中心对称,所以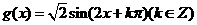 ,所以
,所以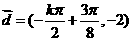 ,
, 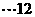 分
分
为使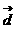 的模最小,则取
的模最小,则取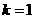 ,此时
,此时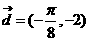
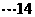 分
分
17.已知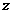 是复数,
是复数,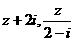 均为实数(
均为实数(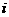 为虚数单位),且复数
为虚数单位),且复数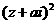 在复平面上对应的点在第一象限,(1)求复数
在复平面上对应的点在第一象限,(1)求复数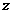 ;(2)求实数
;(2)求实数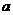 的取值范围。
的取值范围。
解 (1)设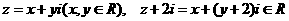
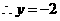
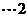 分
分
又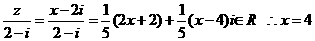
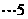 分所以
分所以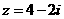 6 分
6 分
(2) 由(1),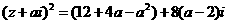
 分
分
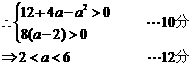
16.设实数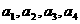 是一个等差数列,且满足
是一个等差数列,且满足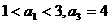 。若定义
。若定义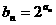 ,给出下列命题:(1)
,给出下列命题:(1)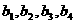 是一个等比数列:(2)
是一个等比数列:(2)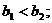 (3)
(3)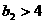 ;(4)
;(4)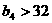 ;
;
(5)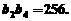 其中真命题的个数为 ( C )
其中真命题的个数为 ( C )
A.2 B.3 C.4 D.5
15.设函数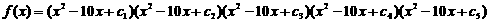
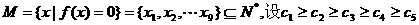 ,则
,则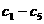 为( C )
为( C )
A.20 B.18 C.16 D.14
14.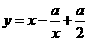 在
在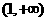 上单调递增,则实数
上单调递增,则实数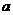 的取值范围是 ( B )
的取值范围是 ( B )
A 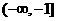 B
B 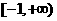 C
C 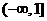 D
D 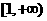
13.题中正确的是 ( C )
A 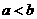 是
是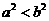 的必要非充分条件;
的必要非充分条件;
B 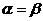 是
是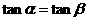 的充分非必要条件
的充分非必要条件
C 两虚数之积为实数是这两虚数互为共轭复数的必要非充分条件;
D 空间两直线不相交是这两直线异面的充要条件。
18.
12.平面上三点,向量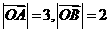 ,设
,设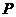 是线段
是线段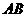 垂直平分线上一点,则
垂直平分线上一点,则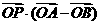 的值为____
的值为____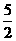 _____________
_____________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com