
题目列表(包括答案和解析)
3.解⑴设等差数列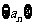 的公差是
的公差是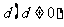 因为
因为
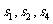 成等比数列,所以
成等比数列,所以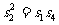 ……………………………………2分
……………………………………2分
即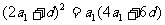 化简得
化简得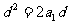 又
又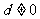 所以
所以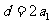 ……5分
……5分
所以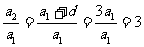 ……………………………………7分
……………………………………7分
⑵因为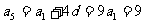
所以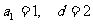 ……………………………………9分
……………………………………9分
所以 ……………………………………11分
……………………………………11分
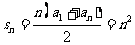 …………………………………13分
…………………………………13分
2.⑴因为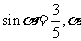 是第二象限角
是第二象限角
所以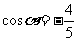 ……………………………………4分
……………………………………4分
从而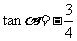 ……………………………………7分
……………………………………7分
⑵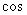
 …………………………13分
…………………………13分
1.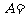
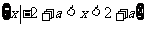 ……………………………………4分
……………………………………4分
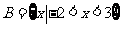 又
又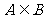 ……………………………………8分
……………………………………8分
所以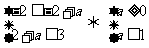 所以
所以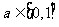 …………………………………13分
…………………………………13分
12. (本小题满分16分) 已知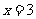 是函数
是函数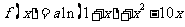 的一个极值点。
的一个极值点。
(Ⅰ)求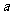 ;(Ⅱ)求函数
;(Ⅱ)求函数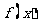 的单调区间;(Ⅲ)若直线
的单调区间;(Ⅲ)若直线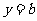 与函数
与函数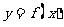 的图象有3个交点,求
的图象有3个交点,求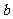 的取值范围。
的取值范围。 

11. (本小题满分16分)已知数列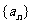 ,其前n项和Sn满足
,其前n项和Sn满足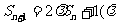 是大于0的
是大于0的
常数),且a1=1,a3=4.
(1)求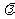 的值;
的值;
(2)求数列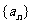 的通项公式an;
的通项公式an; 

(3)设数列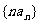 的前n项和为Tn,试比较
的前n项和为Tn,试比较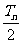 与Sn的大小.
与Sn的大小.
10. (本小题满分16分) 已知DABC的三个内角A,B,C对应的边长分别为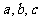 ,向量
,向量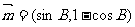 与向量
与向量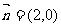 夹角
夹角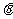 余弦值为
余弦值为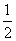 。
。
(1)求角B的大小;(2)DABC外接圆半径为1,求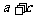 范围
范围 

9. (本小题满分14分)某房地产开发商投资81万元建一座写字楼,第一年装修费为1万元,以后每年增加2万元,把写字楼出租,每年收入租金30万元.
(1)若扣除投资和装修费,则从第几年开始获取纯利润? 

(2)若干年后开发商为了投资其他项目,有两种处理方案:①纯利润总和最大时,以10万元出售;②该楼年平均利润最大时以46万元出售该楼,问哪种方案更优?
8.(本小题满分14分)
设函数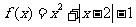 ,
,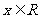
(1)判断函数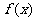 的奇偶性;
的奇偶性; 

(2)求函数的最小值.
7. (本小题满分14分)
已知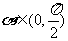 ,
,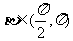 ,
,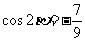 ,
,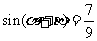 .
. 

(Ⅰ)
求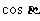 的值;
的值;
(Ⅱ) 求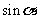 的值.
的值.
6. (12分)已知数列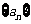 中,
中,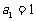 ,前
,前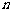 项和为
项和为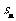 ,当
,当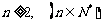 ,
,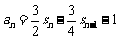
⑴求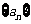 的通项公式;
的通项公式;
⑵设数列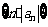 的前
的前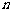 项和为
项和为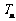 ,若对任意
,若对任意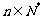 ,都有
,都有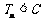 ,求正整数
,求正整数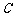 的最小值;
的最小值;
⑶证明:对一切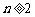 ,
,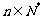 时,
时,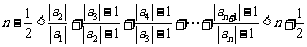
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com