
题目列表(包括答案和解析)
19.解:(Ⅰ)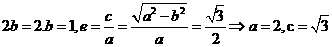
椭圆的方程为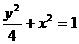 ………………………………3分
………………………………3分
(Ⅱ)由题意,设AB的方程为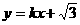
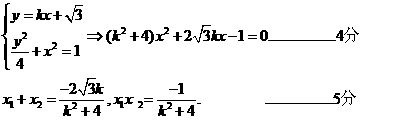
由已知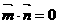 得:
得:
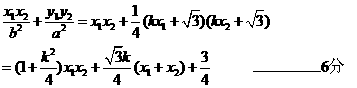
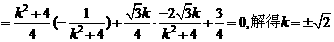 ……7分
……7分
(Ⅲ)
(1)当直线AB斜率不存在时,即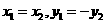 ,由
,由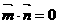
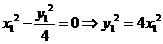 ………………………………8分
………………………………8分
又 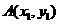 在椭圆上,所以
在椭圆上,所以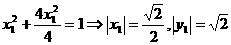
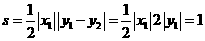
所以三角形的面积为定值. ……………………………………9分
(2)当直线AB斜率存在时:设AB的方程为y=kx+b
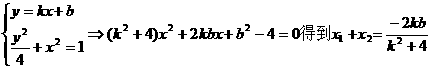
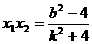 ……………………………………10分
……………………………………10分
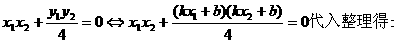
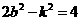 ………………………………………12分
………………………………………12分
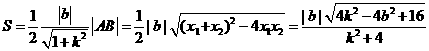
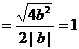
所以三角形的面积为定值.
18.解:(Ⅰ)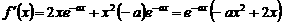 2分
2分
令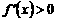 ,∵
,∵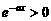 3分∴
3分∴ ,解得
,解得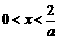 .
4分
.
4分
∴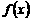 在
在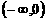 和
和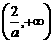 内是减函数,在
内是减函数,在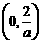 内是增函数.
6分
内是增函数.
6分
(Ⅱ)①当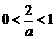 ,即
,即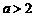 时,
时,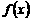 在
在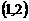 内是减函数.
内是减函数.
∴在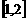 上
上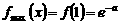 ;
8分
;
8分
②当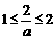 ,即
,即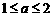 时,
时,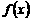 在
在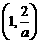 内是增函数,在
内是增函数,在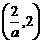 内是减函数.
内是减函数.
∴在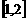 上
上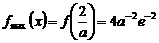 ;
10分
;
10分
③当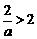 ,即
,即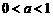 时,
时,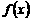 在
在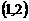 是增函数.
是增函数.
∴在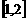 上
上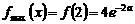 .
12分
.
12分
综上所述,当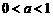 时,
时,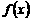 在
在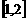 上的最大值为
上的最大值为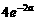 ;当
;当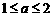 时,
时,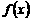 在
在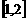 上的最大值为
上的最大值为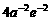 ;当
;当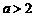 时,
时,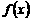 在
在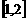 上的最大值为
上的最大值为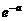 .
13分
.
13分
17.解:(Ⅰ)由题意,区域U内共有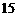 个整点,区域V内共有
个整点,区域V内共有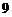 个整点,设所取3个整点中恰有2个整点在区域V的概率为
个整点,设所取3个整点中恰有2个整点在区域V的概率为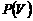 ,则
,则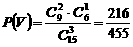 .
6分
.
6分
(Ⅱ)区域U的面积为8,区域V的面积为4,
∴在区域U内任取一点,该点在区域V内的概率为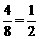 . 8分
. 8分
X的取值为0,1,2,3. 9分
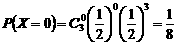 ,
,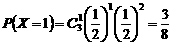 ,
,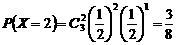 ,
,
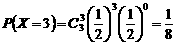 .
11分
.
11分
∴X的分布列为
|
X |
0 |
1 |
2 |
3 |
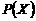 |
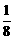 |
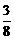 |
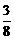 |
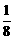 |
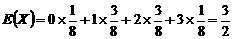 .
13分
.
13分
解:法一:
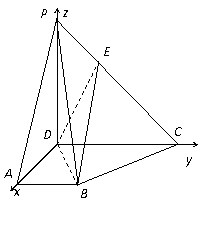
证明:建立如图所示的坐标系,
 (Ⅰ)
(Ⅰ)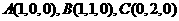 ,
,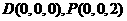 ……………………………1分
……………………………1分
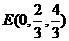
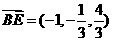 ,
,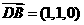 ,
,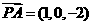
设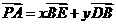 ,可得
,可得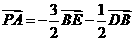
因为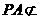 平面
平面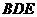 ,所以
,所以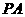 //平面
//平面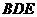 .……3分
.……3分
(Ⅱ)因为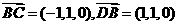 ,所以
,所以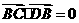
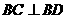 因为
因为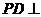 平面
平面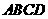 ,所以
,所以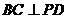
所以 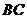
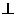 平面
平面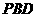 ,所以 平面
,所以 平面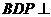 平面
平面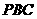 . …………8分
. …………8分
(Ⅲ)因为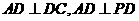
所以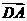 是平面
是平面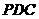 的法向量,
的法向量,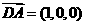 ,设平面
,设平面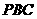 的法向量为
的法向量为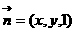 ,
,
由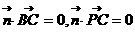 得:
得: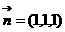 ,设二面角
,设二面角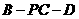 为
为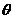 ,
,
则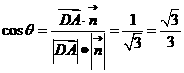 . 所以二面角
. 所以二面角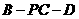 余弦值为
余弦值为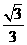 ……14分
……14分
1. B 2.B 3.A 4.D 5.B 6. C 7. D 8.
20.已知数列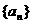 满足:
满足: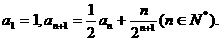
(I)已知数列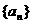 的通项公式;
的通项公式;
(II)证明: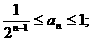
(III)设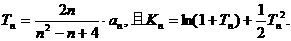 证明:
证明: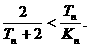
2009-2010北京三十五中高三数学综合测试一(理)解答
19. 设 上的两点,已知向量
上的两点,已知向量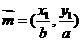 ,
,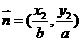 ,若
,若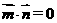 且椭圆的离心率
且椭圆的离心率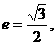 短轴长为
短轴长为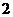 ,
, 为坐标原点.
为坐标原点.
(Ⅰ) 求椭圆的方程;
(Ⅱ)若直线AB过椭圆的焦点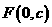 ,(c为半焦距),求直线AB的斜率k的值;
,(c为半焦距),求直线AB的斜率k的值;
(Ⅲ)试问:△AOB的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
18、已知函数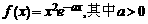 .
.
⑴ 求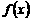 的单调区间;
的单调区间;
⑵ 求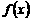 在
在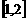 上的最大值.
上的最大值.
17、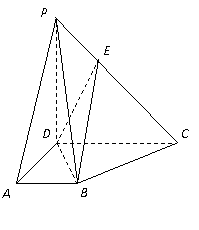 如图:
如图: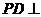 平面
平面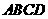 ,四边形ABCD为直角梯形,
,四边形ABCD为直角梯形,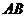 //
//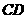 ,
,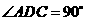 ,
,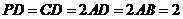 ,,
,,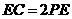 .
.
⑴ 求证: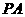 //平面
//平面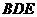 ;
;
⑵ 求证:平面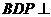 平面
平面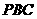 ;
;
⑶ 求二面角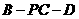 的余弦值.
的余弦值.
16、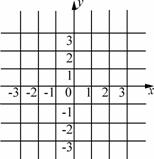 设不等式组
设不等式组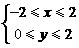 确定的平面区域为
确定的平面区域为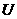 ,
,
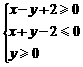 确定的平面区域为
确定的平面区域为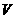 .
.
⑴ 定义坐标为整数的点为“整点”.在区域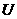 内
内
任取3个整点,求这些整点中恰有2个整点在区域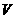 的概率;
的概率;
⑵ 在区域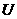 内任取3个点,记此3个点在区域
内任取3个点,记此3个点在区域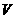 的个数为
的个数为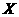 ,求
,求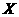 的概率分布列及其
的概率分布列及其
数学期望.
15、已知函数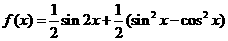
⑴ 求函数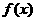 的最小正周期;
的最小正周期;
⑵ 在锐角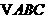 中,若
中,若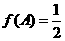 ,
,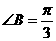 ,
,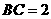 ,求
,求 的长.
的长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com