
题目列表(包括答案和解析)
5.棱台上、下底面面积之比为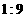 ,则棱台的中截面分棱台成两部分的体积之比是(
)
,则棱台的中截面分棱台成两部分的体积之比是(
)
 A.
A.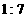 B.
B.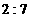 C.
C.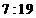 D.
D.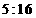
4.圆台的一个底面周长是另一个底面周长的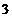 倍,母线长为
倍,母线长为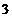 ,圆台的侧面积为
,圆台的侧面积为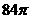 ,则圆台较小底面的半径为( )
,则圆台较小底面的半径为( )
A.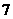 B.
B.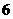 C.
C.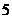 D.
D.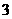
3.一个正方体的顶点都在球面上,它的棱长为 ,则球的表面积是( )
,则球的表面积是( )
A. B.
B. C.
C. D.
D.
2.半径为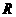 的半圆卷成一个圆锥,则它的体积为( )
的半圆卷成一个圆锥,则它的体积为( )
A.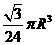 B.
B.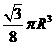 C.
C.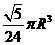 D.
D.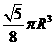
1.如果一个水平放置的图形的斜二测直观图是一个底面为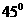 ,腰和上底均为
,腰和上底均为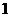 的等腰梯形,那么原平面图形的面积是( )
的等腰梯形,那么原平面图形的面积是( )
A. 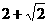 B.
B. 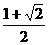 C.
C. 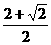 D.
D. 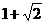
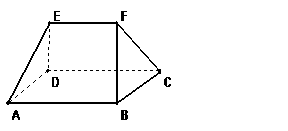
2、解:(1)∵AD=2AB=2,E是AD的中点,
∴△BAE,△CDE是等腰直角三角形,
易知, ∠BEC=90°,即BE⊥EC.
又∵平面D′EC⊥平面BEC,面D′EC∩面BEC=EC,
∴BE⊥面D′EC,又C D′Ì 面D′EC , ∴BE⊥CD′;
(2)法一:设M是线段EC的中点,过M作MF⊥BC
 垂足为F,连接D′M,D′F,则D′M⊥EC.
垂足为F,连接D′M,D′F,则D′M⊥EC.
∵平面D′EC⊥平面BEC,
∴D′M⊥平面EBC,
∴MF是D′F在平面BEC上的射影,由三垂线定理得:
D′F⊥BC
∴∠D′FM是二面D′-BC-E的平面角.
在Rt△D′MF中,D′M=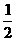 EC=
EC=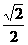 ,MF=
,MF=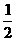 AB=
AB=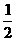
∴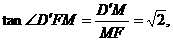
即二面角D′-BC-E的正切值为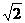 .
.
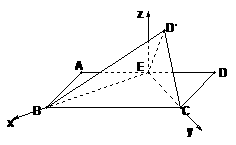
法二:如图,以EB,EC为x轴、y轴,过E垂直于平面BEC的射线为z轴,建立空间直角坐标系.
则B(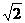 ,0,0),C(0,
,0,0),C(0,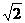 ,0),D′(0,
,0),D′(0,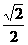 ,
,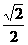 )
)
设平面BEC的法向量为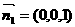 ;平面D′BC的法向量为
;平面D′BC的法向量为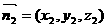
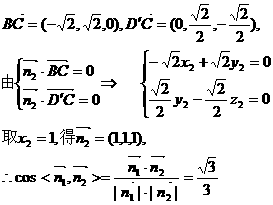
Þ tan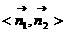 = ∴二面角D′-BC-E的正切值为
= ∴二面角D′-BC-E的正切值为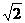 .
.
1、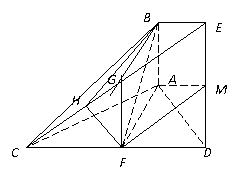 方法一:
方法一:
(1) 证法一:取 的中点
的中点 ,连
,连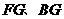 .
.
∵ 为
为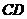 的中点,∴
的中点,∴ 且
且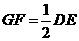 . …………1分
. …………1分
∵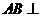 平面
平面 ,
,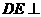 平面
平面 ,
,
∴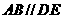 ,∴
,∴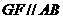 .
…………2分
.
…………2分
又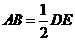 ,∴
,∴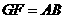 .
…………3分
.
…………3分
∴四边形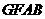 为平行四边形,则
为平行四边形,则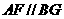 . …………4分
. …………4分
∵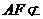 平面
平面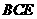 ,
,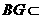 平面
平面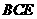 ,
,
∴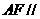 平面
平面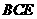 .
…………5分
.
…………5分
证法二:取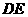 的中点
的中点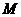 ,连
,连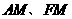 .
.
∵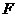 为
为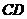 的中点,∴
的中点,∴ .
…………1分
.
…………1分
∵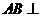 平面
平面 ,
,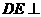 平面
平面 ,∴
,∴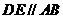 .
…………2分
.
…………2分
又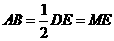 ,
,
∴四边形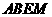 为平行四边形,则
为平行四边形,则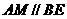 .
…………3分
.
…………3分
∵ 平面
平面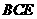 ,
,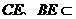 平面
平面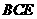 ,
,
∴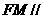 平面
平面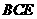 ,
,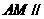 平面
平面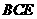 .
.
又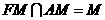 ,∴平面
,∴平面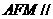 平面
平面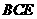 .
…………4分
.
…………4分
∵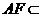 平面
平面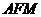 ,
,
∴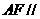 平面
平面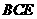 .
…………5分
.
…………5分
(2) 证:∵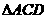 为等边三角形,
为等边三角形,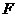 为
为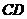 的中点,∴
的中点,∴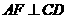 . …………6分
. …………6分
∵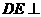 平面
平面 ,
,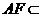 平面
平面 ,∴
,∴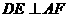 .
…………7分
.
…………7分
又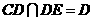 ,故
,故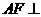 平面
平面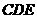 .
…………8分
.
…………8分
∵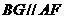 ,∴
,∴ 平面
平面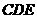 .
…………9分
.
…………9分
∵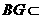 平面
平面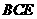 ,
,
 ∴平面
∴平面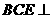 平面
平面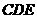 .
…………10分(3)
.
…………10分(3)
解:在平面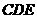 内,过
内,过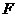 作
作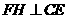 于
于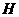 ,连
,连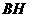 .
.
∵平面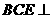 平面
平面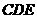 , ∴
, ∴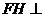 平面
平面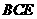 .
.
∴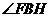 为
为 和平面
和平面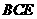 所成的角. …………12分
所成的角. …………12分
设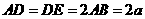 ,则
,则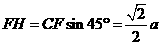 ,
,
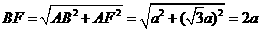 ,
,
R t△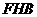 中,
中, .
.
 ∴直线
∴直线 和平面
和平面 所成角的正弦值为
所成角的正弦值为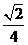 . ……14分
. ……14分
方法二:
设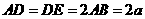 ,建立如图所示的坐标系
,建立如图所示的坐标系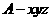 ,则
,则
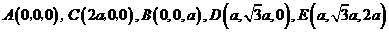 .…………2分
.…………2分
∵ 为
为 的中点,∴
的中点,∴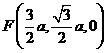 .
…………3分
.
…………3分
(1) 证: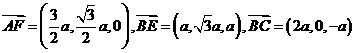 , …………4分
, …………4分
∵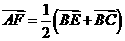 ,
,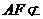 平面
平面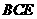 ,∴
,∴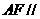 平面
平面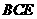 . …………5分
. …………5分
(2) 证:∵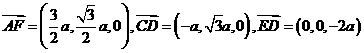 ,
…………6分
,
…………6分
∴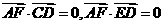 ,∴
,∴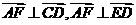 . …………8分
. …………8分
∴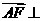 平面
平面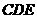 ,又
,又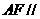 平面
平面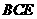 ,
,
∴平面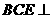 平面
平面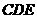 . …………10分
. …………10分
(3) 解:设平面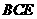 的法向量为
的法向量为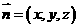 ,由
,由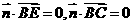 可得:
可得:
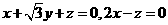 ,取
,取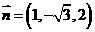 . …………12分
. …………12分
又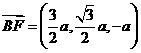 ,设
,设 和平面
和平面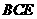 所成的角为
所成的角为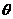 ,则
,则
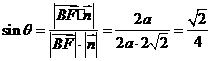 .
.
∴直线 和平面
和平面 所成角的正弦值为
所成角的正弦值为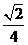 .
…………14分
.
…………14分
5.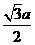
4. 注意
注意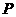 在底面的射影是斜边的中点
在底面的射影是斜边的中点
3.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com