
题目列表(包括答案和解析)
1.给定下列四个命题:
①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.
其中,为真命题的是( )
A.①和② B.②和③ C.③和④ D.②和④
23、对于函数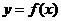 ,定义:若存在非零常数
,定义:若存在非零常数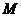 、
、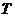 ,使函数
,使函数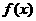 对定义域内的任意实数
对定义域内的任意实数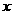 ,都满足
,都满足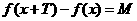 ,则称函数
,则称函数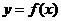 是准周期函数,常数
是准周期函数,常数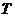 称为函数
称为函数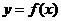 的一个准周期.如:函数
的一个准周期.如:函数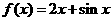 是以
是以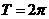 为一个准周期且
为一个准周期且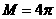 的准周期函数.
的准周期函数.
 (1)
试判断
(1)
试判断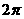 是否是函数
是否是函数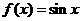
的准周期,说明理由;
(2) 证明函数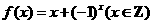 是
是
准周期函数,并求出它的一个准周期
和相应的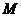 的值;
的值;
(3)请你给出一个准周期函数(不同于题
设和(2)中函数),指出它的一个准周
期和一些性质,并画出它的大致图像.
(1) 
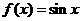 ,
,
∴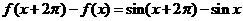
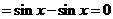 ,
,
∴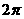 不是函数
不是函数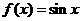 的准周期.
(3分)
的准周期.
(3分)
(2) 
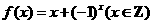 ,
,
∴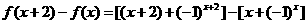
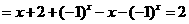 (非零常数),
(3分)
(非零常数),
(3分)
∴函数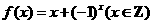 是准周期函数,
是准周期函数,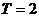 是它的一个准周期,相应的
是它的一个准周期,相应的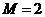 .
(5分)
.
(5分)
(3)①写出一个不同于题设和(2)中函数,
如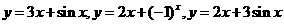 ,
,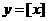 等 得1分
等 得1分
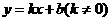 ,
, 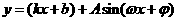 ,
,
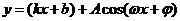 ,
, ,或其它一次函数(正比例函数)与周期函数的线性组合的具体形式,得3分
,或其它一次函数(正比例函数)与周期函数的线性组合的具体形式,得3分
②指出所写出函数的一个准周期,得2分
③指出它的一些性质,如定义域、值域、奇偶性、单调性、最值、 ,
,
(写出一条得1分,两条以上得2分,可以不证明)
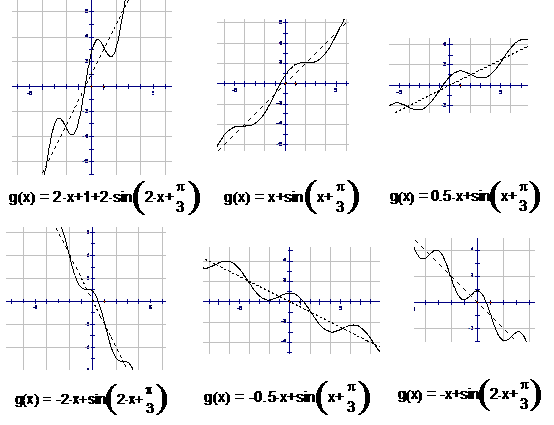
④画出其大致图像. 得3分
部分参考图像:
22、设数列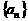 的前n项和为
的前n项和为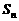 ,已知
,已知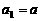 (
(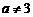 ),
),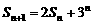 ,
,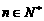 .
.
(1)设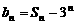 ,
,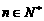 ,证明数列
,证明数列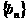 为等比数列;
为等比数列;
(2)求数列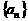 的通项公式;
的通项公式;
(3)若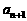 ≥
≥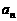 ,
,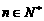 ,求a的取值范围.
,求a的取值范围.
(1)当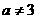 时,
时,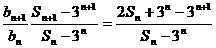 =2
=2
所以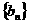 为等比数列。
为等比数列。
(2)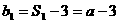 ,
, 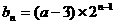 。
。
所以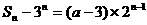
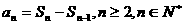
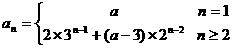 ;
;
(3)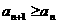 ,
,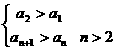 ,
,
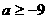 所以
所以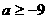 ,且
,且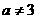 。
。
21、已知角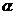 的顶点在原点,始边与
的顶点在原点,始边与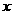 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点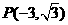 .
.
(1)解关于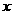 的方程:
的方程: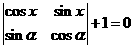 ;
;
(2)若函数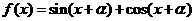 (
( )的图像关于直线
)的图像关于直线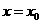 对称,求
对称,求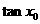 的值.
的值.
(1) 角
角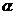 终边经过点
终边经过点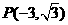 ,∴
,∴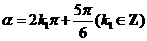 .
.
∴由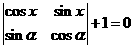 可得:
可得: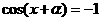
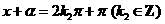 ,
∴
,
∴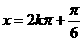
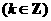 .
.
(2)
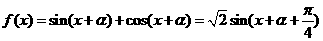 (
( )
)
且函数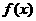 的图像关于直线
的图像关于直线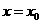 对称,
对称,
∴ 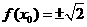 ,即
,即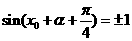 , ∴
, ∴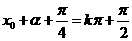 ,
,
即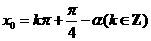 ∴
∴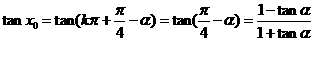
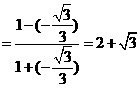 .
.
20、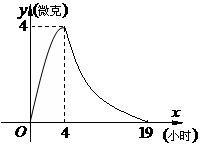 某医药研究所开发一种新药,据监测:服药后每毫升血液中的含药量
某医药研究所开发一种新药,据监测:服药后每毫升血液中的含药量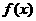 与时间
与时间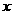 之间满足如图所示曲线.当
之间满足如图所示曲线.当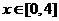 时,所示的曲线是二次函数图像的一部分,满足
时,所示的曲线是二次函数图像的一部分,满足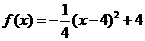 ,当
,当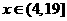 时,所示的曲线是函数
时,所示的曲线是函数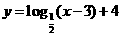 的图像的一部分.据测定:每毫升血液中含药量不少于
的图像的一部分.据测定:每毫升血液中含药量不少于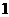 微克时治疗疾病有效.请你算一下,服用这种药一次大概能维持多长的有效时间?(精确到
微克时治疗疾病有效.请你算一下,服用这种药一次大概能维持多长的有效时间?(精确到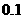 小时)
小时)
由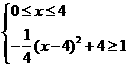 ,解得:
,解得: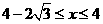 ①
①
由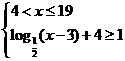 ,解得:
,解得: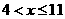 ②
②
由①、②知: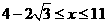 ,
,

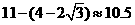 ,
,
∴服用这种药一次大概能维持的有效时间为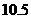 小时.
小时.
19、如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,
PA⊥底面ABCD,PA=4,M为PA的中点,N为BC的中点.
(文科)(1)求四棱锥P-ABCD的体积;
(2)求异面直线PC与MD所成角的大小.
(理科)(1)求点B到平面PCD的距离;
(2)求二面角M-ND-A的大小.
(文科)(1)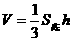 =
=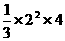 =
=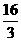 ;
;
(2)连ME,则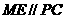 ,因此
,因此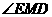 即为异面直线MD与PC所成角。
即为异面直线MD与PC所成角。
计算得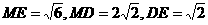
所以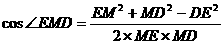 =
=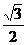 ,
,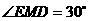
(理科)(1)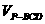 =
=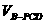 ,计算得
,计算得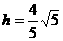 。
。
(2)二面角M-ND-A的大小为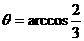
18、对于函数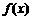 定义域中任意的
定义域中任意的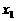 ,
,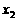
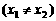 ,有如下结论:
,有如下结论:
①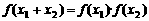 ;②
;②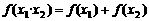 ;③
;③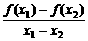 >0;
>0;
④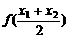 <
<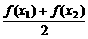 .
.
当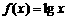 时,上述结论中正确结论的序号是………………………………………( C
)
时,上述结论中正确结论的序号是………………………………………( C
)
 (A) ①② (B)
③④ (C)
②③ (D)
②④
(A) ①② (B)
③④ (C)
②③ (D)
②④
17、给定空间中的平面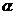 及平面
及平面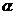 的一条斜线
的一条斜线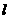 .条件“直线
.条件“直线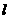 与平面
与平面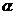 内无数条直线
内无数条直线
成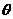 角”是“直线
角”是“直线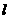 与平面
与平面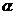 成
成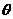 角”的
[答]( B )
角”的
[答]( B )
(A) 充分非必要条件. (B) 必要非充分条件.
(C) 充要条件. (D) 既非充分也非必要条件.
16、如图为函数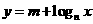 的图像,其中
的图像,其中 、
、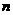 为常数,则下列结论正确的是
为常数,则下列结论正确的是
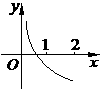 [答]( D )
[答]( D )
(A) 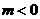 ,
,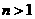 . (B)
. (B) 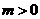 ,
,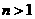 .
.
(C) 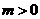 ,
,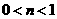 . (D)
. (D) 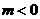 ,
,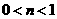 .
.
15、已知 ( C )
( C )
(A) 1+2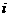 (B)
1-2
(B)
1-2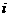 (C)
2+
(C)
2+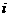 (D)
2-
(D)
2-
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com