
题目列表(包括答案和解析)
20、[解](1)证明:由 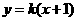 得
得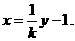
将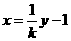 代入
代入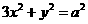 消去
消去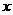 得
得
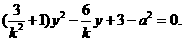 ① ………………………… 3分
① ………………………… 3分
由直线l与椭圆相交于两个不同的点得
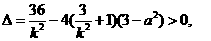 整理得
整理得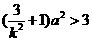 ,即
,即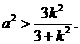 ………5分
………5分
(2)解:设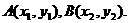 由①,得
由①,得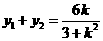
∵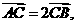 而点
而点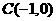 , ∴
, ∴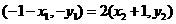
得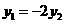 代入上式,得
代入上式,得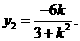 ……………8分
……………8分
于是,△OAB的面积
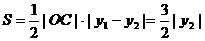
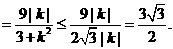 --------11分
--------11分
其中,上式取等号的条件是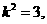 即
即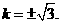 ……………………12分
……………………12分
由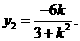 可得
可得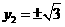
将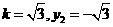 及
及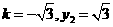 这两组值分别代入①,均可解出
这两组值分别代入①,均可解出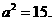
∴△OAB的面积取得最大值的椭圆方程是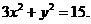 --------------14分
--------------14分
20、设直线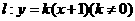 与椭圆
与椭圆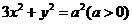 相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点.
相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点.
(1)证明: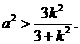 ;
;
(2)若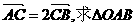 的面积取得最大值时的椭圆方程.
的面积取得最大值时的椭圆方程.
19、[解](Ⅰ)因为四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,
则CD⊥侧面PAD
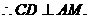 又
又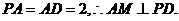
又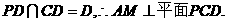 ……………5分
……………5分
(Ⅱ)建立如图所示的空间直角坐标系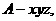 又PA=AD=2,
又PA=AD=2,
则有P(0,0,2),D(0,2,0)
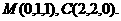
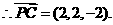
设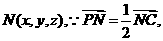 则有
则有
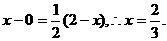
同理可得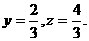
即得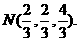 …………………………8分
…………………………8分
由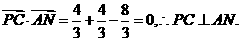

而平面PAB的法向量可为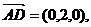
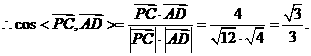
故所求平面AMN与PAB所成锐二面角的余弦值为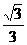 ……13分
……13分
19、如图,已知四棱锥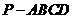 的底面是正方形,
的底面是正方形,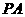 ⊥底面
⊥底面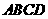 ,且
,且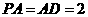 ,点
,点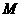 、
、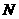 分别在侧棱
分别在侧棱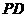 、
、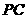 上,且
上,且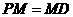
(Ⅰ)求证: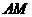 ⊥平面
⊥平面 ;
;
(Ⅱ)若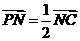 ,求平面
,求平面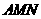 与平面
与平面 的所成锐二面角的余弦值。
的所成锐二面角的余弦值。
18、[解] (Ⅰ)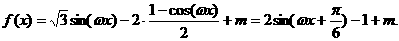 ……2分
……2分
依题意函数
所以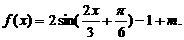 …………4分
…………4分

(Ⅱ)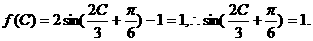
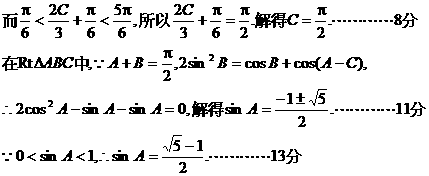
18、已知函数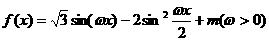 的最小正周期为
的最小正周期为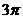 ,当
,当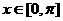 时,函数
时,函数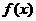 的最小值为0.
的最小值为0.
(Ⅰ)求函数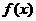 的表达式;
的表达式;
(Ⅱ)在△ABC中,若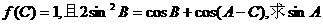 的值.
的值.
17、在数列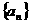 中,如果存在非零常数T,使得
中,如果存在非零常数T,使得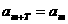 对任意正整数m均成立,那么就称
对任意正整数m均成立,那么就称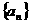 为周期数列,其中T叫做数列
为周期数列,其中T叫做数列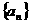 的周期. 已知数列
的周期. 已知数列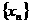 满足
满足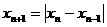 (
(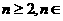 N
N ),且
),且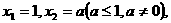 当数列
当数列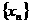 周期为3时,则该数列的前2007项的和为
1338
周期为3时,则该数列的前2007项的和为
1338
16、设某几何体的三视图如下(尺寸的长度单位为m)。
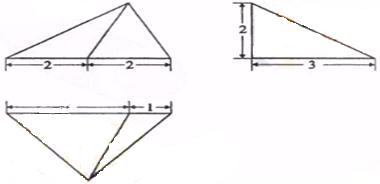
则该几何体的体积为 4
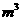 。
。
15、若函数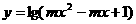 的定义域为R则m的取值范围____________13.0
的定义域为R则m的取值范围____________13.0 m<4
m<4
14、已知平面向量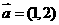 ,
,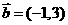 ,
,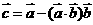 ,则
,则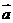 与
与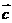 夹角的余弦值为 。
夹角的余弦值为 。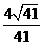
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com