
题目列表(包括答案和解析)
2. 关于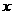 的不等式(
的不等式(
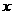 -1)(
-1)(
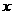 -2)>0,若此不等式的解集为{
-2)>0,若此不等式的解集为{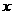 |
|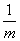 <x<2},则
<x<2},则 的取值范围是
的取值范围是
 A.
A.  >0
B.0<
>0
B.0< <2
C.
<2
C.  >
>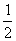 D.
D.  <0
<0
解析:由不等式的解集形式知m<0. 答案:D
考点2 含参数不等式的解法
题型1:解含参数有理不等式
例1:解关于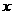 的一元二次不等式
的一元二次不等式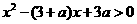
[解题思路]比较根的大小确定解集
解析:∵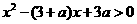 ,∴
,∴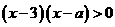
⑴当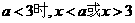 ,不等式解集为
,不等式解集为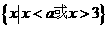 ;
;
⑵当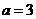 时,不等式为
时,不等式为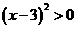 ,解集为
,解集为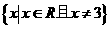 ;
;
⑶当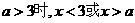 ,不等式解集为
,不等式解集为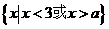
[名师指引]解含参数的有理不等式时分以下几种情况讨论:①根据二次项系数(大于0,小于0,等于0);②根据根的判别式讨论(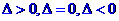 ).③根据根的大小讨论(
).③根据根的大小讨论(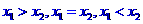 ).
).
题型2:解简单的指数不等式和对数不等式
例2. 解不等式loga(1-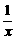 )>1
)>1 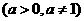
[解题思路]借助于单调性进行分类讨论
解析(1)当a>1时,原不等式等价于不等式组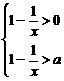
 由此得1-a>
由此得1-a>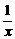 .因为1-a<0,所以x<0,∴
.因为1-a<0,所以x<0,∴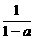 <x<0.
<x<0.
(2)当0<a<1时,原不等式等价于不等式组: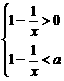
由 ①得x>1或x<0,由②得0
<x<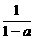 ,∴1<x<
,∴1<x<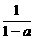 .
.
综上,当a>1时,不等式的解集是{x|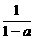 <x<0
<x<0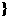 ,当0<a<1时,不等式的解集为{x|1<x<
,当0<a<1时,不等式的解集为{x|1<x<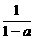 }.
}.
[名师指引]解指数不等式与对数不等式通常是由指数函数和对数函数的单调性转化为一般的不等式(组)来求解,当底数含参数时要进行分类讨论.
[新题导练]
1.不等式(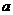 -2)
-2)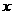 2+2(
2+2(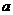 -2) -4<0,对一切
-2) -4<0,对一切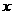 ∈R恒成立,则a的取值范围是( )
∈R恒成立,则a的取值范围是( )
A.(-∞,2] B.(-2,2] C.(-2,2) D.(-∞,2)
解析:∵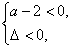 可推知-2<a<2,另a=2时,原式化为-4<0,恒成立,∴-2<a≤2. 选B
可推知-2<a<2,另a=2时,原式化为-4<0,恒成立,∴-2<a≤2. 选B
10. (汕头金山中学09届高三11月考)在 中,内角
中,内角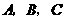 对边的边长分别是
对边的边长分别是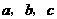 ,已知
,已知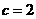 ,
,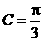 .
.
(Ⅰ)若 的面积等于
的面积等于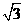 ,求
,求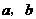 ;
;
(Ⅱ)若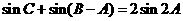 ,求
,求 的面积.
的面积.
解:(Ⅰ)由余弦定理及已知条件得,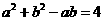 ,
,
又因为 的面积等于
的面积等于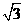 ,所以
,所以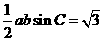 ,得
,得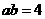 .
.
联立方程组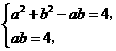 解得
解得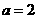 ,
,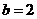 .
.
(Ⅱ)由题意得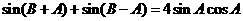 ,
,
即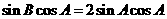 ,当
,当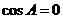 时,
时,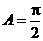 ,
,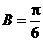 ,
,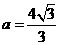 ,
,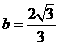 ,
,
当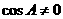 时,得
时,得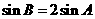 ,由正弦定理得
,由正弦定理得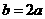 ,
,
联立方程组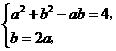 解得
解得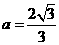 ,
,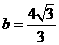 .
.
所以 的面积
的面积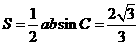 .
.
|

|
版权所有:()
版权所有:()
9. 在△ABC中,若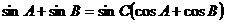 .
.
(1)判断△ABC的形状;
(2)在上述△ABC中,若角C的对边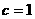 ,求该三角形内切圆半径的取值范围。
,求该三角形内切圆半径的取值范围。
解:(1)由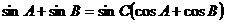
可得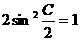
 即C=90°
即C=90°
 △ABC是以C为直角顶点得直角三角形
△ABC是以C为直角顶点得直角三角形
(2)内切圆半径
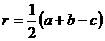
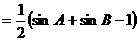
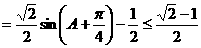
 内切圆半径的取值范围是
内切圆半径的取值范围是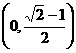
8.在锐角三角形中,边a、b是方程x2-2x+2=0的两根,角A、B满足:
2sin(A+B)-=0,求△ABC的面积。
解:由2sin(A+B)-=0,得sin(A+B)=, ∵△ABC为锐角三角形
∴A+B=120°, C=60°, 又∵a、b是方程x2-2x+2=0的两根,∴a+b=2,
a·b=2, ∴c2=a2+b2-2a·bcosC=(a+b)2-3ab=12-6=6,
∴c=, 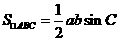 =×2×= 。
=×2×= 。
7.在△ABC中,已知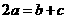 ,
,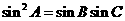 ,试判断△ABC的形状。
,试判断△ABC的形状。
解:由正弦定理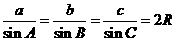 得:
得: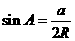 ,
,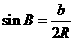 ,
,
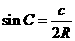 。
。
所以由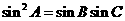 可得:
可得: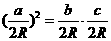 ,即:
,即: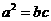 。
。
又已知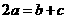 ,所以
,所以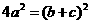 ,所以
,所以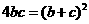 ,即
,即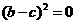 ,
,
因而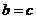 。故由
。故由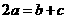 得:
得: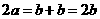 ,
,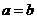 。所以
。所以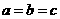 ,△ABC
,△ABC
为等边三角形。
6.在△ABC中,已知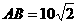 ,A=45°,BC=
,A=45°,BC=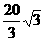 ,求角C。
,求角C。
解:由正弦定理得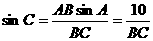 ,又BC=
,又BC=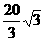 时,故 sinC=
时,故 sinC=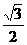 ;
;
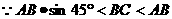
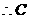 有两解
有两解 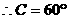 或120°
或120°
综合拔高训练
5.在△ABC中,a、b、c分别是角A、B、C的对边, 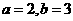 ,
, 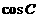 =
=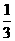 ,则其外接圆的半径为_______________.
,则其外接圆的半径为_______________.
[解析]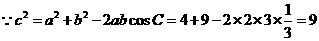 ,
,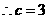
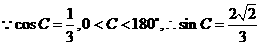
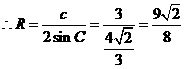
4. 若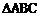 中,
中,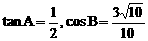 ,则角C的大小是__________
,则角C的大小是__________
解析
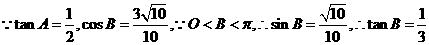
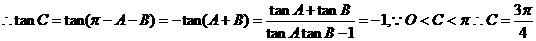
3.在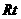 △ABC中,C=
△ABC中,C=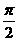 ,则
,则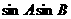 的最大值是_______________.
的最大值是_______________.
[解析] ∵在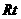 △ABC中,C=
△ABC中,C=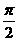 ,∴
,∴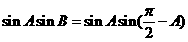

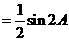 ,∵
,∵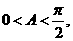 ∴
∴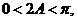 ∴
∴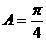 时,
时,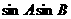 取得最大值
取得最大值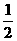 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com