
题目列表(包括答案和解析)
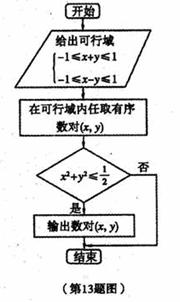
13.在可行城内任取一点,规则如右边的流程图所示,则能
输出数对(x,y)的概率是
22.解:(1) 由题设可得动点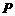 的轨迹方程为
的轨迹方程为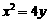 . ………………4分
. ………………4分
(2) 由(1),可设直线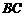 的方程为:
的方程为: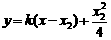
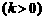 ,
,
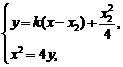 消
消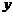 得,
得,
易知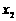 、
、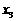 为该方程的两个根,故有
为该方程的两个根,故有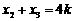 ,得
,得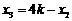 ,
,
从而得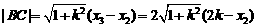 , ……………………6分
, ……………………6分
类似地,可设直线 的方程为:
的方程为: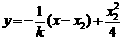 ,
,
从而得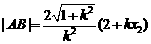 ,
……………………8分
,
……………………8分
由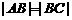 ,得
,得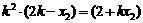 ,
,
解得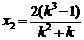 ,
,
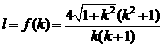
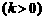 . ……………………10分
. ……………………10分
(3) 因为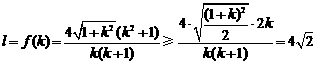 ,……………………12分
,……………………12分
所以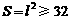 ,即
,即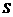 的最小值为
的最小值为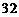 ,
,
当且仅当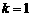 时取得最小值.……………………14分
时取得最小值.……………………14分
21.解:(1) ∵ 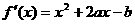 ,k.s.5.u
,k.s.5.u
∴ 由题意可知: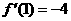 且
且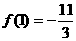 ,
,
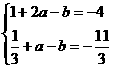 解得
解得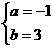 ……………………3分
……………………3分
∴ 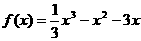
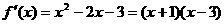
令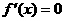 ,得
,得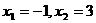
由此可知:
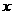 |
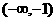 |
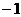 |
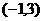 |
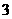 |
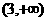 |
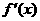 |
+ |
 |
- |
 |
+ |
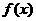 |
↗ |
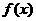 极大 极大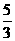 |
↘ |
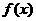 极小 极小 |
↗ |
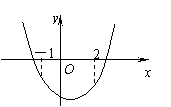 ∴ 当
∴ 当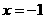 时,
时, 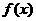 取极大值
取极大值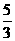 . ………………………… 6分
. ………………………… 6分
(2) ∵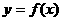 在区间
在区间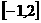 上是单调减函数,
上是单调减函数,
∴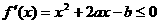 在区间[-1,2]上恒成立.
在区间[-1,2]上恒成立.
根据二次函数图象可知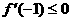 且
且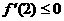 ,
,
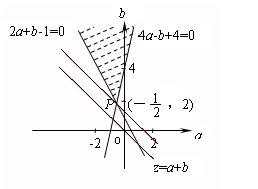 即:
即: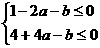 也即
也即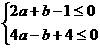 ……9分
……9分
作出不等式组表示的平面区域如图:
当直线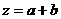 经过交点
经过交点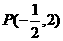 时,
时,
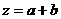 取得最小值
取得最小值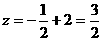 ,
,
∴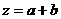 取得最小值为
取得最小值为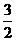 ……………………12分
……………………12分
20. 解:(1)设该学生选修甲、乙、丙的概率分别为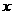 、
、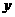 、
、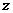
依题意得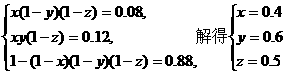 …………3分
…………3分
若函数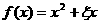 为
为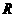 上的偶函数,则
上的偶函数,则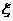 =0
=0
当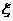 =0时,表示该学生选修三门功课或三门功课都没选.
=0时,表示该学生选修三门功课或三门功课都没选.
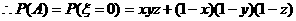
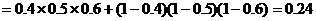
∴事件 的概率为
的概率为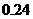 ………… 6分k.s.5.u
………… 6分k.s.5.u
(2)依题意知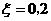 ………… 8分
………… 8分
则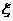 的分布列为
的分布列为
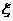 |
0 |
2 |
|
P |
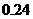 |
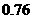 |
∴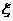 的数学期望为
的数学期望为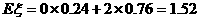 …………12分
…………12分
19.解:(1)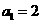 ,
,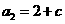 ,
,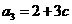 ,
,
因为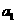 ,
,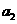 ,
,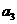 成等比数列,…………2分
成等比数列,…………2分
所以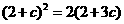 ,
,
解得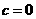 或
或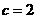 .…………5分k.s.5.u
.…………5分k.s.5.u
当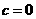 时,
时,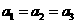 ,不符合题意舍去,故
,不符合题意舍去,故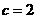 .…………6分
.…………6分
(2)当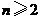 时,由于
时,由于
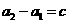 ,
,
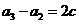 ,
,

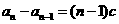 ,
,
所以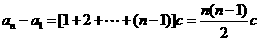 .…………10分
.…………10分
又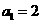 ,
,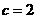 ,故
,故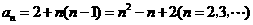 .
.
当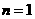 时,上式也成立,
时,上式也成立,
所以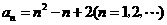 .…………12分k.s.5.u
.…………12分k.s.5.u
18.解: (1) 如图建立空间直角坐标系.设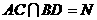 ,
,
 连结
连结 ,则
,则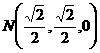 …………2分
…………2分
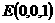 ∴
∴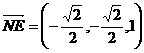
又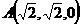 ,
,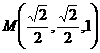
∴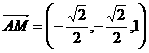 …………4分
…………4分
∴ 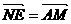 且
且 与
与 不共线,k.s.5.u
不共线,k.s.5.u
∴ ∥
∥ ,又
,又
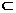 平面
平面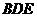 ,
,
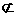 平面
平面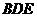 ,
,
∴ ∥平面
∥平面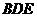 .
…………6分
.
…………6分
(2) 设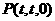
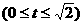 ,
,
则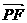 =,
=, 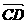 =.
=.
又∵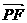 与
与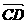 所成的角为60°,………… 8分
所成的角为60°,………… 8分
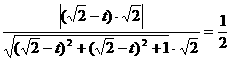 ,………… 9分
,………… 9分
解之得(舍去),…………11分
故点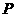 为
为 的中点. …………12分
的中点. …………12分
17.解:(1)∵∣a∣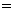 1 ,∣b∣
1 ,∣b∣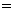 1
……1分
1
……1分
∣a-b∣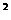
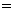 ∣a∣
∣a∣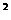 -2a﹒b
-2a﹒b 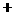 ∣b∣
∣b∣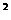
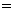 ∣a∣
∣a∣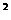
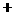 ∣b∣
∣b∣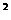 -
-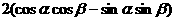
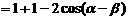
∣a–b∣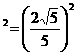
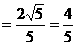 . ……4分
. ……4分
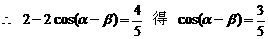 ……6分
……6分
(2)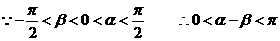 ……7分
……7分
由 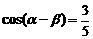 得
得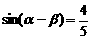 ……8分
……8分
由 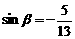 得
得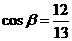 ……10分
……10分
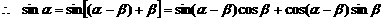 ……11分
……11分
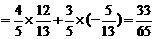 ……12分
……12分
22.(本小题满分14分)
(1) 已知动点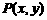 到点
到点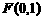 与到直线
与到直线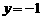 的距离相等,求点
的距离相等,求点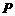 的轨迹
的轨迹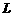 的方程;
的方程;
(2) 若正方形 的三个顶点
的三个顶点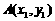 ,
,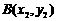 ,
,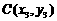 (
(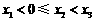 )在(1)中的曲线
)在(1)中的曲线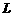 上,设
上,设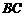 的斜率为
的斜率为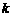 ,
, ,求
,求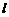 关于
关于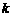 的函数解析式
的函数解析式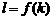 ;
;
(3) 求(2)中正方形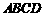 面积
面积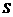 的最小值.
的最小值.
[2010烟台一模]答案
21. (本小题满分12分) k.s.5.u
已知函数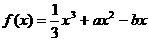 (
(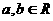 )
)
(1) 若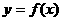 图象上的点
图象上的点 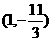 处的切线斜率为
处的切线斜率为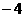 ,求
,求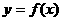 的极大值;
的极大值;
(2) 若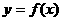 在区间
在区间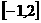 上是单调减函数,求
上是单调减函数,求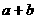 的最小值.
的最小值.
20. (本小题满分12分)
某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响. 已知某学生只选修甲的概率为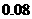 ,只选修甲和乙的概率是
,只选修甲和乙的概率是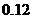 ,至少选修一门的概率是
,至少选修一门的概率是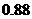 ,用
,用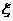 表示该学生选修的课程门数和没有选修的课程门数的乘积.
表示该学生选修的课程门数和没有选修的课程门数的乘积.
(1)记“函数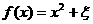
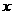 为
为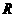 上的偶函数”为事件
上的偶函数”为事件 ,求事件
,求事件 的概率;
的概率;
(2)求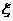 的分布列和数学期望.
的分布列和数学期望.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com