
题目列表(包括答案和解析)
9.将编号为1到5的5个小球放入编号为1到4的4个盒子,每个盒子至少放1个,则恰有1个小球的编号数与盒子的编号数相同的放法种数是 ( )
A.44 B.92 C.108 D.117
8.已知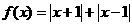 且
且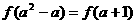 ,则a的值个数是 ( )
,则a的值个数是 ( )
A.2 B.3 C.4 D.无数
7. 若椭圆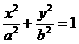 (a>b>0)的离心率
(a>b>0)的离心率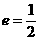 ,右焦点为
,右焦点为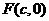 ,方程
,方程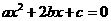 的两个实数根分别是
的两个实数根分别是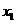 和
和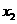 ,则点
,则点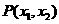 到原点的距离为( )
到原点的距离为( )
A.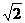 B.
B.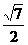 C.2
D.
C.2
D.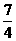
6.已知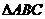 的边AB=4,O为边AB的中点,若P为OC上的动点,则
的边AB=4,O为边AB的中点,若P为OC上的动点,则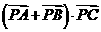 的最小值是( )
的最小值是( )
A 2 B 0 C -2 D -1
5. 已知下列四个命题:
① 若一条直线垂直于一个平面内无数条直线,则这条直线与这个平面垂直;
② 若一条直线平行于一个平面,则垂直于这条直线的直线必垂直于这个平面;
③ 若一条直线平行一个平面,另一条直线垂直这个平面,则这两条直线垂直;
④ 若两条直线垂直,则过其中一条直线有唯一一个平面与另外一条直线垂直;
其中真命题的序号是( )
A.①② B.②③ C.②④ D.③④
4.等差数列{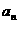 }前n项和为
}前n项和为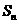 。已知
。已知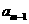 +
+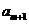 -2
-2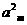 =0,
=0,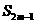 =35,则m的值为( )
=35,则m的值为( )
A.9 B.10 C.18 D.20
3.△ABC中,锐角A满足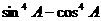 ≤
≤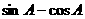 ,则( )
,则( )
A.0<A≤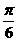 B.0<A≤
B.0<A≤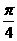 C.
C.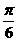 ≤A≤
≤A≤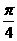 D.
D.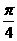 ≤A<
≤A<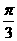
2. 已知集合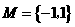 ,
,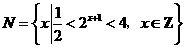 ,则
,则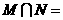 ( )
( )
A.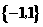 B.
B.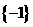 C.
C.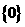 D.
D.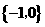
1.已知复数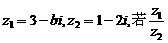 是实数,则实数b的值为( )
是实数,则实数b的值为( )
A.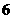 B.
B.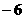 C.0
D.
C.0
D.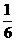
20.解:(Ⅰ)当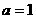 时,
时,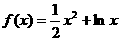 ,
,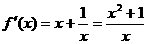 ;
2分
;
2分
对于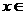 [1,e],有
[1,e],有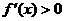 ,∴
,∴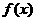 在区间[1,e]上为增函数, 3分
在区间[1,e]上为增函数, 3分
∴ 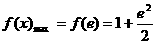 ,
,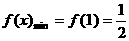 …5分
…5分
(Ⅱ)令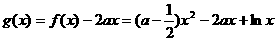 ,则
,则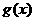 的定义域为(0,+∞) …6分
的定义域为(0,+∞) …6分
在区间(1,+∞)上,函数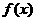 的图象恒在直线
的图象恒在直线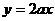 下方等价于
下方等价于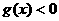 在区间(1,+∞)上恒成立.
在区间(1,+∞)上恒成立.
∵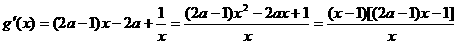
① 若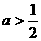 ,令
,令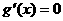 ,得极值点
,得极值点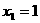 ,
,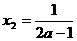 ,
……8分
,
……8分
当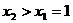 ,即
,即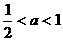 时,在(
时,在(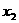 ,+∞)上有
,+∞)上有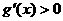 ,
,
此时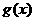 在区间(
在区间(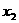 ,+∞)上是增函数,并且在该区间上有
,+∞)上是增函数,并且在该区间上有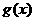 ∈(
∈(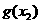 ,+∞),不合题意9分
,+∞),不合题意9分
当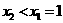 , 即
, 即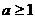 时, 同理可知,
时, 同理可知, 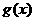 在区间(1, +∞)上,有
在区间(1, +∞)上,有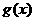 ∈(
∈(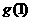 , +∞),也不合题意; …10分
, +∞),也不合题意; …10分
② 若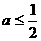 ,则有
,则有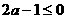 ,此时在区间(1,+∞)上恒有
,此时在区间(1,+∞)上恒有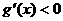 ,
,
从而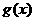 在区间(1,+∞)上是减函数;
……12分
在区间(1,+∞)上是减函数;
……12分
要使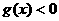 在此区间上恒成立,只须满足
在此区间上恒成立,只须满足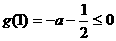
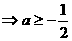 ,
,
由此求得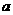 的范围是[
的范围是[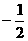 ,
,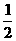 ].
].
综合①②可知,当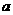 ∈[
∈[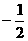 ,
,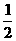 ]时,函数
]时,函数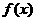 的图象恒在直线
的图象恒在直线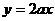 下方 …14分
下方 …14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com