12.已知n条直线l₁:x-y+c₁＝0,l₂:x-y+c₂＝0,…,l_n:x-y+c_n＝0,其中c₁＜c₂＜…＜c_n,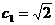,在这n(n≥2)条平行线中,每相邻两条直线之间的距离依次为3,5,7,…,2n-1.

(1)求c_n;

(2)求满足条件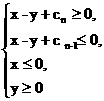的平面区域的面积______________________.

解:(1)|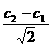|＝3,c₂-c₁＝,

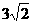同理，c₃-c₂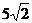＝,…,c_n-c_n-1＝(2n-1),

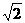c_n＝［(1+3+5+…+(2n-1)］＝.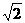

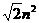(2)平面区域是梯形，高为2n-1,上底为2(n-1)²，下底为2n²,

其面积为S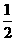＝ (2n-1)［2n²+2(n-1)²］＝4n³-6n²+4n-1.

11.点P(x,y)满足不等式组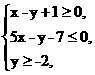i为x轴正方向上的单位向量，则向量OP在向量i方向上的投影的最大值为______________.

解析:画出可行域，其可行域为以A(2,3)、B(-3,-2)、C(1,-2)为顶点的三角形内部部分(包含边界)，过A作x轴的垂线，垂足为D，由图形可知向量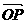在向量i方向上的投影的最大值为OD的长度，即为2.

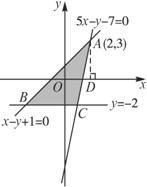
答案:2

10.已知变量x,y满足约束条件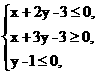若目标函数z＝ax+y(其中a＞0)仅在点(3,0)处取得最大值,则a的取值范围为______________.

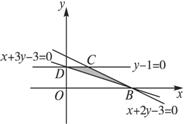
解析:画出可行域如图所示，其中B(3，0)，C(1，1)，D(0，1)，若目标函数z＝ax+y取得最大值，必在B，C，D三点处取得，故有3a＞a+1且3a＞1，解得a＞.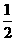

答案:( ,+∞)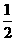

9.已知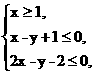则x²+y²的最小值是__________________.

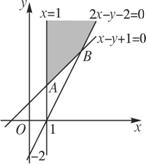
解析: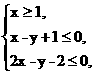画出可行域,得交点A(1,2),B(3,4),则x²+y²的最小值是5.

答案:5

8.(2008全国高考卷Ⅰ,13)若x,y满足约束条件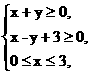则z＝2x-y的最大值为_____________.

解析:如图,作出可行域,

作出直线l₀:2x-y＝0,将l₀平移至过点A处时,函数z＝2x-y有最大值9.

答案:9

7.设O为坐标原点,M(2,1),若N(x,y)满足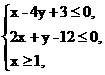则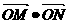取得最大值时，点N的个数是(　　 )

A.1　　 　　　　　　　B.2 　　　　　　　　　C.3　　　 　　　　　　D.无数个

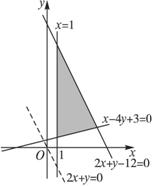
解析:画出可行域如图，设z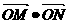＝＝2x+y,当z＝2x+y对应的直线同直线2x+y-12＝0重合时，z最大，此时有无数个点.

答案:D

6.当点M(x,y)在如图所示的三角形ABC内(含边界)运动时,目标函数z＝kx+y取得最大值的一个最优解为(1,2),则实数k的取值范围是(　　 )

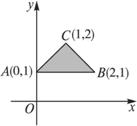
A.(-∞,-1］∪［1,+∞)　　　　　 B.［-1,1］　　　　 C.(-∞,-1)∪(1,+∞)　　　　　 D.(-1,1)

解析:目标函数所表示的直线的斜率为-k,当直线所表示的斜率比直线BC的斜率大,比直线AC的斜率小时,恰好在点C(1,2)处取得最优解.∵k_AC＝1,k_BC＝-1,∴-1≤-k≤1,解得-1≤k≤1.

答案:B

5.在平面直角坐标系xOy中,已知平面区域A＝{(x,y)|x+y≤1,且x≥0,y≥0},则平面区域B＝{(x+y,x-y)|(x,y)∈A}的面积为 ……(　　 )

A.2　　　　　 　　　　　　B.1 　　　　　　　　　C.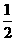　　　　 　　　　　　　D.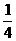

解析:令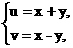∴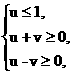作出区域是等腰直角三角形,可求出面积S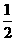＝×2×1＝1,选B.

答案:B

4.在约束条件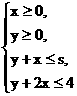下，当3≤s≤5时，目标函数z＝3x+2y的最大值的变化范围是(　　 )

A.［6，15］　　　　 B.［7，15］　　　　　　　　　 C.［6，8］　　　　　　 D.［7，8］

解析:由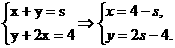交点为A(2,0),B(4-s,2s-4),C(0,s),C′(0,4),

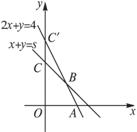
(1)当3≤s＜4时,可行域是四边形OABC,此时,7≤z＜8;

(2)当4≤s≤5时,可行域是△OAC′,此时z_max＝8,故选D.

答案:D

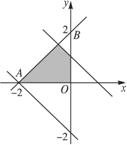
3.(2008安徽高考,文11)若A为不等式组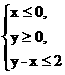表示的平面区域,则当a从-2连续变化到1时,动直线x+y＝a扫过A中的那部分区域的面积为(　　 )

A.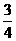　　　　　　 　　　　　　B.1 　　　　　　　　　　C.　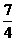　　　　　　　 D.2

解析:如右图,知区域的面积是△OAB去掉一个小直角三角形.

(阴影部分面积比1大,比S_△OAB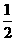＝×2×2＝2小,故选C,不需要算出来)

答案:C