
题目列表(包括答案和解析)
2、(2009昆明市期末)已知数列{an}是公差不为零的等差数列,且a1,a3,a4成等比数列,Sn为数列{an}的前n 项和,则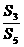 的值为 ( )
的值为 ( )
A.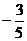 B.
B. C.
C.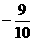 D.
D.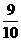
答案 D
1、(2009滨州一模)等差数列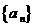 中,
中,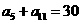 ,
,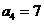 ,则
,则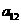 的值为
的值为
A.15 B.23 C.25 D.37
答案 B
18.解(1)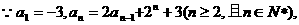
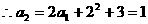
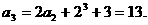
(2)证法一:对于任意
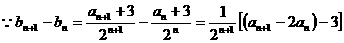
=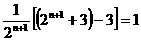 ,
,
 数列
数列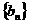 是首项为
是首项为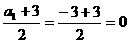 ,公差为1的等差数列.
,公差为1的等差数列.
证法二:(等差中项法)
(3)由(2)得,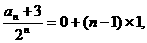
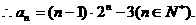
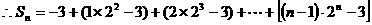 ,
,
即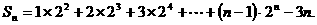
设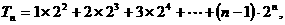
则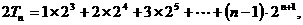
两式相减得,
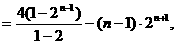
整理得,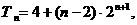
从而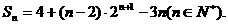
17.(祥云一中二次月考理)(本小题满分12分)
在数列
(1)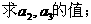
(2)设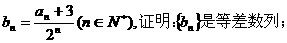
(3)求数列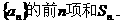

16.
(安庆市四校元旦联考)(本题满分16分)各项均为正数的数列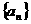 中,
中,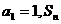 是数列
是数列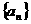 的前
的前 项和,对任意
项和,对任意 ,有
,有
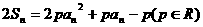 ;
;
⑴求常数 的值;
⑵求数列
的值;
⑵求数列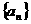 的通项公式;
的通项公式;
⑶记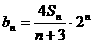 ,求数列
,求数列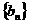 的前
的前 项和
项和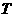 。
。
解:(1)由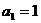 及
及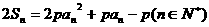 ,得:
,得: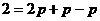
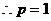 [来源:]
[来源:]
(2)由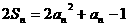 ①
①
得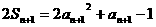 ②
②
由②-①,得 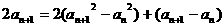
即: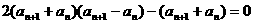

由于数列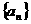 各项均为正数,
各项均为正数,
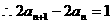 即
即 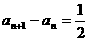
 数列
数列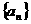 是首项为
是首项为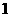 ,公差为
,公差为 的等差数列,
的等差数列,
 数列
数列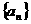 的通项公式是
的通项公式是 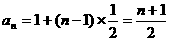
(3)由 ,得:
,得: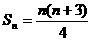
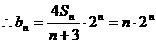
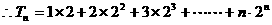

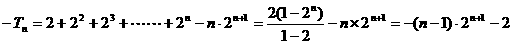

15.(三明市三校联考)(本小题满分13分)
已知数列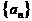 的前
的前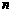 项和为
项和为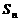 ,
,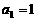 ,且
,且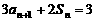 (
(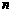 为正整数)
为正整数)
(Ⅰ)求出数列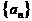 的通项公式;
的通项公式;
(Ⅱ)若对任意正整数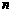 ,
,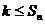 恒成立,求实数
恒成立,求实数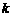 的最大值.
的最大值.
解:(Ⅰ)
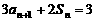 ,
①
,
① 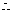 当
当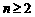 时,
时,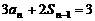 . ②
. ②
由 ① - ②,得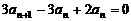 .
. 
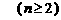 .
.
又 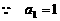 ,
,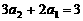 ,解得
,解得
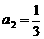 .
.
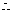 数列
数列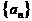 是首项为1,公比为
是首项为1,公比为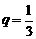 的等比数列.
的等比数列.
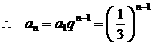 (
(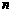 为正整数)
……………………(7分)
为正整数)
……………………(7分)
(Ⅱ)由(Ⅰ)知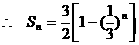
由题意可知,对于任意的正整数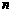 ,恒有
,恒有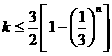 ,.
,.
 数列
数列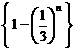 单调递增,
当
单调递增,
当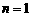 时,数列中的最小项为
时,数列中的最小项为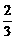 ,
,
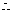 必有
必有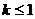 ,即实数
,即实数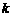 的最大值为1
……………… (13分)
的最大值为1
……………… (13分)
14. (池州市七校元旦调研)在数列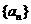 中,
中,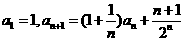 ,
,
(I)设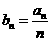 ,求数列
,求数列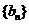 的通项公式;
的通项公式;
(II)求数列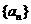 的前
的前 项和
项和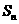
解:(I)由已知有
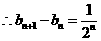
利用累差迭加即可求出数列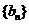 的通项公式:
的通项公式:  (
(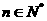 )
)
(II)由(I)知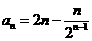 ,
,

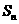 =
=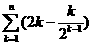
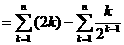
而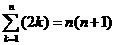 ,又
,又 是一个典型的错位相减法模型,
是一个典型的错位相减法模型,
易得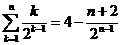

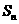 =
=
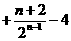
13. (祥云一中三次月考文) 数列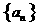 中,
中,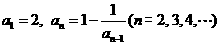 ,则
,则 =
=
答案:2
12.(祥云一中三次月考理)已知数列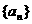 的通项公式为
的通项公式为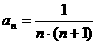 ,数列
,数列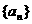 的前
的前 项和为
项和为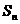 ,则
,则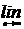
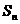 =_________
=_________
答案:1
11.(安庆市四校元旦联考)对于数列{ },定义数列{
},定义数列{ }为数列{
}为数列{ }的
}的
“差数列”,若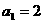 ,{
,{ }的“差数列”的通项
}的“差数列”的通项
为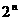 ,则数列{
,则数列{ }的前
}的前 项和
项和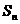 =
=
答案 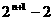
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com