
题目列表(包括答案和解析)
2010年高考题
6. (2009年广东省广州市高三年级调研测试)如图,已知
等腰直角三角形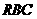 ,其中∠
,其中∠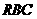 =90º,
=90º,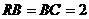 .
.
点A、D分别是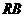 、
、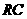 的中点,现将△
的中点,现将△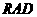 沿着边
沿着边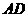
折起到△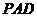 位置,使
位置,使 ⊥
⊥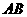 ,连结
,连结 、
、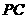 .
.
(1)求证: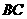 ⊥
⊥ ;
;
(2)求二面角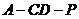 的平面角的余弦值.
的平面角的余弦值.
(1)证明 ∵点A、D分别是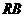 、
、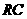 的中点,
的中点,
∴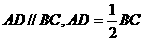 .
.
∴∠ =90º.
=90º.
∴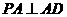 .
.
∴ 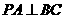 ,
,
∵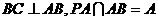 ,
,
∴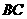 ⊥平面
⊥平面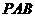 .
.
∵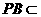 平面
平面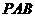 ,
,
∴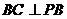 .
.
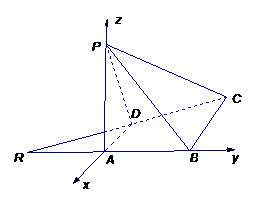 (2)解 建立如图所示的空间直角坐标系
(2)解 建立如图所示的空间直角坐标系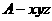 .
.
则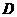 (-1,0,0),
(-1,0,0),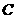 (-2,1,0),
(-2,1,0),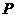 (0,0,1).
(0,0,1).
∴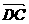 =(-1,1,0),
=(-1,1,0),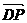 =(1,0,1),
=(1,0,1),
设平面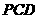 的法向量为
的法向量为 =(x,y,z),则:
=(x,y,z),则:
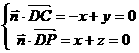 ,
,
令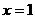 ,得
,得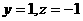 ,
,
∴ =(1,1,-1).
=(1,1,-1).
显然,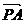 是平面
是平面 的一个法向量,
的一个法向量,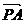 =(
=(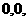
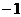 ).
).
∴cos< ,
,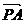 >=
>=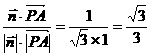 .
.
∴二面角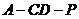 的平面角的余弦值是
的平面角的余弦值是 .
.
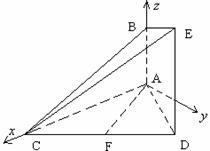
5.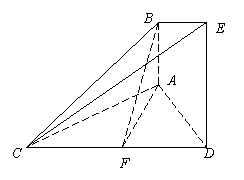 (广东省高明一中2009届高三上学期第四次月考)如图,
(广东省高明一中2009届高三上学期第四次月考)如图,
已知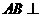 平面
平面 ,
, 平面
平面 ,△
,△ 为
为
等边三角形,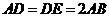 ,
,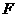 为
为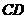 的中点.
的中点.
(1) 求证: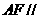 平面
平面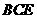 ;
;
(2) 求证:平面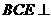 平面
平面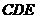 ;
;
(3) 求直线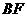 和平面
和平面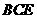 所成角的正弦值.
所成角的正弦值.
 设
设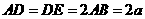 ,建立如图所示的坐标系
,建立如图所示的坐标系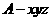 ,则
,则
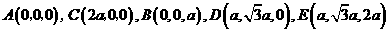 .
.
∵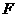 为
为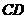 的中点,∴
的中点,∴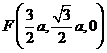 .
.
(1) 证明 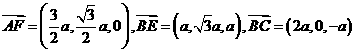 ,
,
∵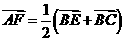 ,
,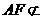 平面
平面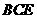 ,∴
,∴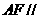 平面
平面 .
.
(2) 证明 ∵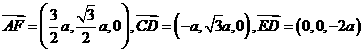 ,
,
∴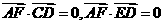 ,∴
,∴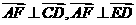 .
.
∴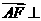 平面
平面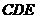 ,又
,又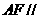 平面
平面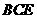 ,
,
∴平面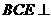 平面
平面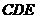 .
.
(3) 解 设平面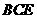 的法向量为
的法向量为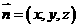 ,由
,由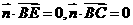 可得:
可得:
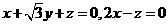 ,取
,取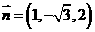 .
.
又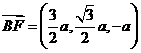 ,设
,设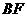 和平面
和平面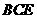 所成的角为
所成的角为 ,则
,则
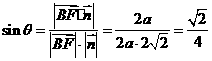 .
.
 ∴直线
∴直线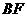 和平面
和平面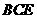 所成角的正弦值为
所成角的正弦值为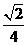 .
.
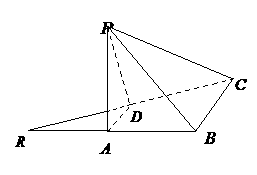
4. (广东省北江中学2009届高三上学期12月月考)如图,
(广东省北江中学2009届高三上学期12月月考)如图,
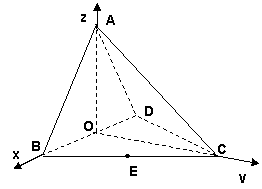
在四面体ABCD中,O、E分别是BD、BC的中点,
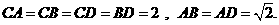
(1)求证: 平面BCD;
平面BCD;
(2)求异面直线AB与CD所成角的余弦值;
(3)求点E到平面ACD的距离.
⑴ 证明 连结OC
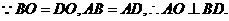
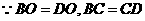 ,
,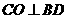 .
.
在 中,由已知可得
中,由已知可得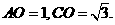
而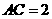 ,
, 
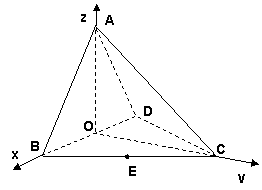
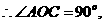 即
即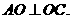
 ∴
∴ 平面
平面 .
.
(2)解 以O为原点,如图建立空间直角坐标系,
则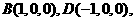
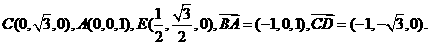
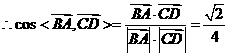 ,
,
∴
异面直线AB与CD所成角的余弦值为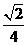 .
.
⑶解 设平面ACD的法向量为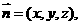 则
则
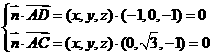 ,
,
∴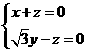 ,令
,令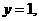 得
得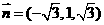 是平面ACD的一个法向量.
是平面ACD的一个法向量.
又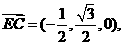 ∴点E到平面ACD的距离
∴点E到平面ACD的距离 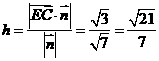 .
.
3.(厦门市第二外国语学校2008-2009学年高三数学第四次月考)已知点H在正方体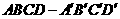 的对角线
的对角线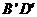 上,∠HDA=
上,∠HDA= .
.
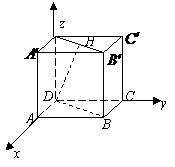 (Ⅰ)求DH与
(Ⅰ)求DH与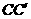 所成角的大小;
所成角的大小;
(Ⅱ)求DH与平面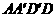 所成角的大小.
所成角的大小.
解:以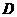 为原点,
为原点, 为单位长建立空间直角坐标系
为单位长建立空间直角坐标系 .
.
设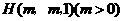
则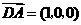 ,
,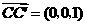 .连结
.连结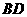 ,
,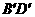 .
.
设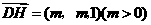 ,由已知
,由已知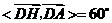 ,
,
由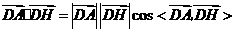
可得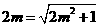 .解得
.解得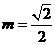 ,
,
所以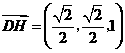 .(Ⅰ)因为
.(Ⅰ)因为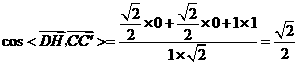 ,
,
所以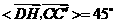 .即DH与
.即DH与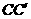 所成的角为
所成的角为 .
.
(Ⅱ)平面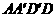 的一个法向量是
的一个法向量是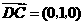 .
.
因为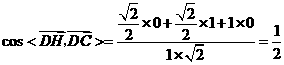 , 所以
, 所以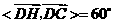 .
.
可得DH与平面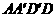 所成的角为
所成的角为 .
.
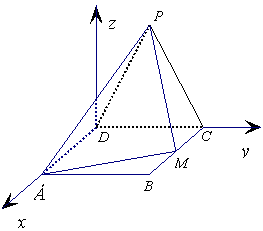
2. (陕西省西安铁一中2009届高三12月月考)如图,边长为2的等
边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=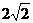 ,
,
M为BC的中点
(Ⅰ)证明:AM⊥PM ;
(Ⅱ)求二面角P-AM-D的大小;
 (Ⅲ)求点D到平面AMP的距离。
(Ⅲ)求点D到平面AMP的距离。
(Ⅰ) 证明 以D点为原点,分别以直线DA、DC为x轴、y轴,
建立如图所示的空间直角坐标系 ,
,
依题意,可得
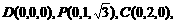
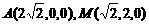
∴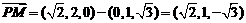
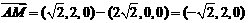
∴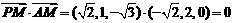
即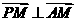 ,∴AM⊥PM .
,∴AM⊥PM .
(Ⅱ)解 设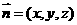 ,且
,且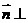 平面PAM,则
平面PAM,则
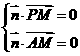 即
即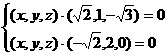
∴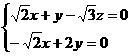 ,
, 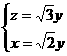
取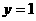 ,得
,得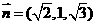
取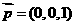 ,显然
,显然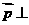 平面ABCD, ∴
平面ABCD, ∴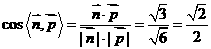
结合图形可知,二面角P-AM-D为45°;
(Ⅲ) 设点D到平面PAM的距离为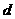 ,由(Ⅱ)可知
,由(Ⅱ)可知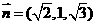 与平面PAM垂直,则
与平面PAM垂直,则
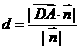 =
=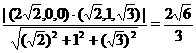
即点D到平面PAM的距离为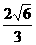
1.
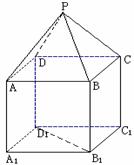
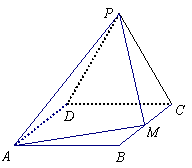
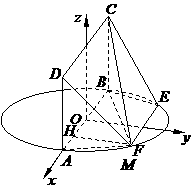
 (湖南省衡阳市八中2009届高三第三次月考试题)如图,P-ABCD是正四棱锥,
(湖南省衡阳市八中2009届高三第三次月考试题)如图,P-ABCD是正四棱锥,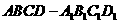 是正方体,其中
是正方体,其中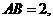
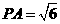
(1)求证: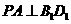 ;
;
(2)求平面PAD与平面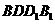 所成的锐二面角
所成的锐二面角 的余弦值;
的余弦值;
(3)求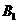 到平面PAD的距离
到平面PAD的距离
以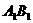 为
为 轴,
轴,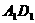 为
为 轴,
轴, 为
为 轴建立空间直角坐标系
轴建立空间直角坐标系
(1)证明 设E是BD的中点, P-ABCD是正四棱锥,∴
P-ABCD是正四棱锥,∴
又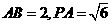 , ∴
, ∴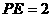 ∴
∴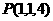 ∴
∴ 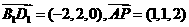
∴ 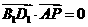 , 即
, 即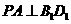 。
。
(2)解 设平面PAD的法向量是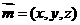 ,
,
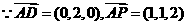
∴ 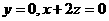 取
取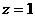 得
得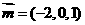 ,又平面
,又平面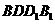 的法向量是
的法向量是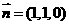 ∴
∴ 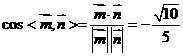 , ∴
, ∴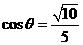 。
。
 (3)解
(3)解 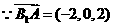 ∴
∴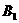 到平面PAD的距离
到平面PAD的距离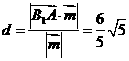 。
。
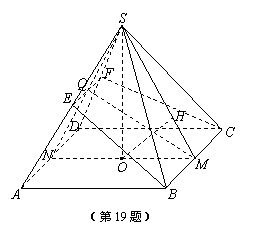
7、(2009南华一中12月月考)正四棱锥S-ABCD中,O为底面中心,E为SA的中点,AB=1,直线AD到平面SBC的距离等于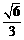 .
.
(1)求斜高SM的长;
(2)求平面EBC与侧面SAD所成锐二面角的小;
解法一:(1)连OM,作OH⊥SM于H.
∵SM为斜高,∴M为BC的中点,
∴BC⊥OM.
∵BC⊥SM,∴BC⊥平面SMO.
又OH⊥SM,∴OH⊥平面SBC. 2分
由题意,得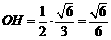 .
.
设SM=x,
则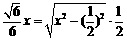 ,解之
,解之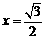 ,即
,即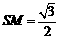 .…………………6分
.…………………6分
(2)设面EBC∩SD=F,取AD中点N,连SN,设SN∩EF=Q.
∵AD∥BC,∴AD∥面BEFC.而面SAD∩面BEFC=EF,∴AD∥EF.
又AD⊥SN,AD⊥NM,AD⊥面SMN.
从而EF⊥面SMN,∴EF⊥QS,且EF⊥QM.
∴∠SQM为所求二面角的平面角,记为α.……… 7分
由平几知识,得 .
.
 ∴
∴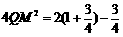 ,∴
,∴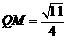 .
.
∴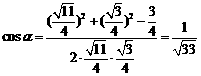 ,即
,即
所求二面角为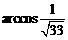 .
……… 12分
.
……… 12分
解法二:(1)建立空间坐标系(如图)
∵底面边长为1,∴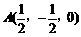 ,
,
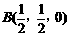 ,
,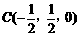 ,
,
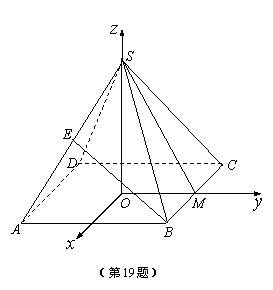
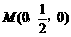 . ……………1分
. ……………1分
设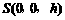 ,
,
平面SBC的一个法向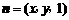 ,
,
则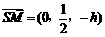 ,
,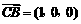 .
.
∴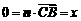 ,
,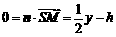 .
.
∴y=2h,n=(0,2h,1).… 3分
而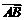 =(0,1,0),由题意,得
=(0,1,0),由题意,得
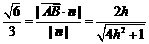 .解得
.解得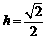 .
.
∴斜高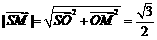 .
…………………………………………6分
.
…………………………………………6分
(2)n=(0,2h,1)=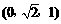 ,
,
由对称性,面SAD的一个法向量为n1=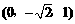 ………8分
………8分
设平面EBC的一个法向量n2=(x,y,1),由
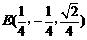 ,
,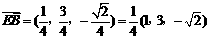 ,得
,得
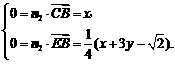 解得
解得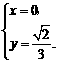 ∴
∴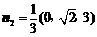 .…10分
.…10分
设所求的锐二面角为α,则
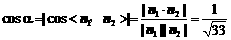 ,∴
,∴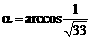 .……… 12分
.……… 12分
2009年联考题
6、(2009昆明市期末)如图,在正三棱柱ABC-A1B1C1中,BB1=2,BC=2 ,D为B1C1的中点。
,D为B1C1的中点。
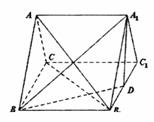 (Ⅰ)证明:B1C⊥面A1BD;
(Ⅰ)证明:B1C⊥面A1BD;
(Ⅱ)求二面角B-AC-B1的大小。
方法一:
(Ⅰ)证明:在Rt△BB1D和Rt△B1C1C中,
由
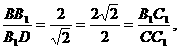 得
得
△BB1D∽△B1C1C,∠B1DB=∠B1CC1。
又 ∠CB1D+∠B1CC1=90°
故 ∠CB1D+∠B1DB=90°
故 B1C⊥BD.·····················3分
又 正三棱柱ABC-A1B1C1,D为B1C1的中点。
由 A1D⊥平面B1C,
得 A1D⊥B1C
又A1D∩B1D=D,
所以 B1C⊥面A1BD。···················································6分
(Ⅱ)解:设E为AC的中点,连接BE、B1E。
在正三棱柱ABC-A1B1C1中,B1C=B1A,∴B1E⊥AC,BE⊥AC,
即 ∠BEB1为二面角B-AC-B1的平面角·································9分
又
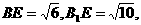
故
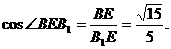
所以 二面角的大小为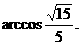 ······································12分
······································12分
方法二:
(Ⅰ)证明:设BC的中点为O,如图建立空间直角坐标系O-xyz
依题意有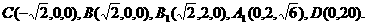
则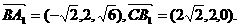
由
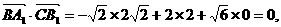
故 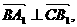
又 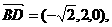
所以
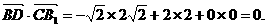
故
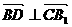 又 BD∩BA1=B
又 BD∩BA1=B
所以 B1C⊥面A1BD,
(Ⅱ)依题意有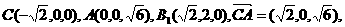
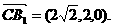
设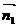 ⊥平面ACB1,
⊥平面ACB1,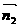 ⊥平面ABC。
⊥平面ABC。
求得
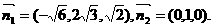
故
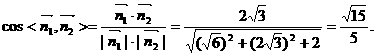
所以 二面角的大小为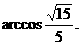 ······································12分
······································12分
5、(2009深圳一模)如图,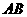 为圆
为圆 的直径,点
的直径,点 、
、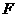 在圆
在圆 上,
上,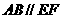 ,矩形
,矩形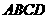 和圆
和圆 所在的平面互相垂直.已知
所在的平面互相垂直.已知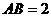 ,
,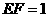 .
.
(Ⅰ)求证:平面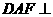 平面
平面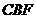 ;
;
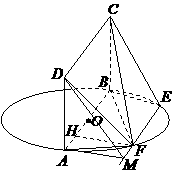 (Ⅱ)求直线
(Ⅱ)求直线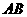 与平面
与平面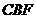 所成角的大小;
所成角的大小;
(Ⅲ)当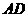 的长为何值时,二面角
的长为何值时,二面角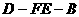 的大小为
的大小为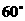 ?
?
解:(Ⅰ)证明: 平面
平面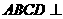 平面
平面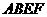 ,
,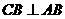 ,
,
平面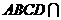 平面
平面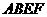 =
=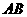 ,
,
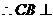 平面
平面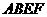 .
.
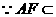 平面
平面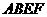 ,
,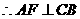 ,
,
又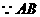 为圆
为圆 的直径,
的直径,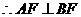 ,
,
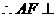 平面
平面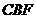 .
.
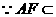 平面
平面 ,
, 平面
平面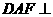 平面
平面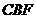 . …………………4分
. …………………4分
(Ⅱ)根据(Ⅰ)的证明,有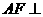 平面
平面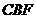 ,
,
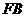 为
为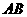 在
在
平面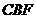 上的射影,
上的射影,
因此,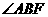 为直线
为直线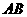 与平面
与平面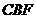 所成的角.
………………………5分
所成的角.
………………………5分
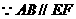 ,
, 四边形
四边形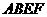 为等腰梯形,
为等腰梯形,
过点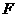 作
作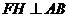 ,交
,交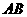 于
于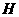 .
.
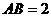 ,
,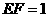 ,则
,则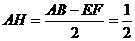 .
.
在 中,根据射影定理
中,根据射影定理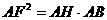 ,得
,得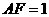 .…………………7分
.…………………7分
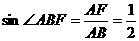 ,
,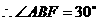 .
.
 直线
直线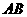 与平面
与平面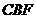 所成角的大小为
所成角的大小为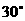 .
…………………8分
.
…………………8分
(Ⅲ)(解法一)过点 作
作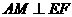 ,交
,交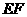 的延长线于点
的延长线于点 ,连
,连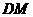 .
.
根据(Ⅰ)的证明,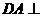 平面
平面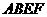 ,则
,则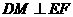 ,
,
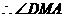 为二面角
为二面角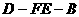 的平面角,
的平面角,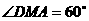 .…………………9分
.…………………9分
在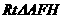 中,
中,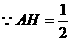 ,
,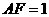 ,
,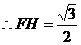 . ………………… 10分
. ………………… 10分
又 四边形
四边形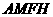 为矩形,
为矩形,
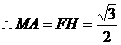 .
.
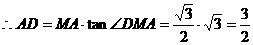 .
.
因此,当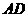 的长为
的长为 时,二面角
时,二面角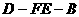 的大小为
的大小为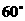 . …………………12分
. …………………12分
 (解法二)设
(解法二)设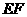 中点为
中点为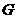 ,以
,以 为坐标原点,
为坐标原点, 、
、 、
、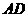 方向
方向
分别为 轴、
轴、 轴、
轴、 轴方向建立空间直角坐标系(如图)
轴方向建立空间直角坐标系(如图)
设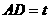
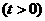 ,则点
,则点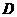 的坐标为
的坐标为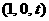
在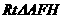 中,
中,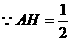 ,
,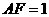 ,
,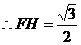 .
.
 点
点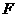 的坐标为
的坐标为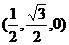 ,点
,点 的坐标为
的坐标为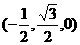 ,
,
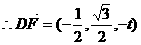 ,
,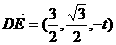
设平面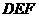 的法向量为
的法向量为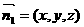 ,则
,则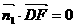 ,
,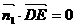 .
.
即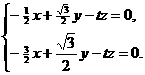 令
令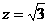 ,解得
,解得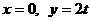
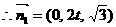 …………………10分
…………………10分
取平面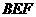 的一个法向量为
的一个法向量为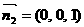 ,依题意
,依题意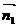 与
与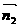 的夹角为
的夹角为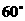
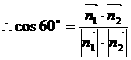 ,即
,即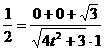 ,
解得
,
解得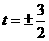 (负值舍去)
(负值舍去)
因此,当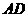 的长为
的长为 时,二面角
时,二面角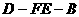 的大小为
的大小为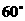 . …………………12分
. …………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com