13．(2009·广东深圳)已知点P(sinπ，cosπ)落在角θ的终边上，且0≤θ≤2π，则θ＝________.

答案：

解析：∵θ∈[0,2π)，根据三角函数定义可知：

sinθ＝cos＝sin(2π+－)＝sin，∴θ＝.

12．(2010·福建师大附中期中考试)函数y＝sinx和y＝tanx的图象在[－2π，2π]上交点的个数为　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．3　 　　　　　 B．5 　　　　　 C．7　 　　　　　 D．9

答案：B

解析：方法一：图象法，在同一坐标系内画y＝sinx与y＝tanx在[0,2π]上的图象．，由图知共有5个交点，故选B.

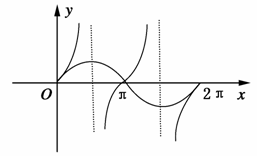
方法二：解方程sinx＝tanx，即tanx(cosx－1)＝0，∴tanx＝0或cosx＝1，∵x∈[－2π，2π]，∴x＝0，±π，±2π，故有5个解，因此选B.

第Ⅱ卷(非选择题　共90分)

11．已知f(x)＝sin(2x+φ)+cos(2x+φ)为奇函数，且在[0，]上为减函数，则φ的一个值为　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.　 　　　　　　 B.π　 　　　　　 C.π　 　　　　　 D.

答案：D

解析：f(x)＝2sin(2x+φ+)，要使f(x)是奇函数，必须φ+＝kπ(k∈Z)，

因此应排除A、B.

当φ＝时f(x)＝2sin2x在[0，]上为增函数，

故C不对．

当φ＝时，f(x)＝－2sin2x在[0，]上为减函数．故选D.

10．(2009·安徽，8)已知函数f(x)＝sinwx+coswx(w＞0)，y＝f(x)的图象与直线y＝2的两个相邻交点的距离等于π，则f(x)的单调递增区间是　　　　　　　　　　　　　　　　　　　　　　 (　)

A．[kπ－，kπ+]，k∈Z

B．[kπ+，kπ+]，，k∈Z

C．[kπ－，kπ+]，k∈Z

D．[kπ+，kπ+]，k∈Z

答案：C

解析：f(x)＝sinwx+coswx

＝2sin(wx+)，(w＞0)．

∵f(x)的图象与直线y＝2的两个相邻交点的距离等于π，恰好是f(x)的一个周期，

∴＝π，w＝2.

f(x)＝2sin(2x+)．

故其单调增区间应满足2kπ－≤2x+≤2kπ+，k∈Z.kπ－≤x≤kπ+，故选C.

9．(2009·浙江台州)已知函数f(x)＝2sin(wx+φ)(w＞0,0＜φ＜π)，且函数的图象如图所示，则点(w，φ)的坐标是　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

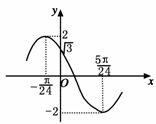
A．(2，)　 　　　　　　　　　　　　　　　 B．(4，)

C．(2，)　 　　　　　　　　　　　　　　 D．(4，)

答案：D

解析：由图象可知：函数的半个周期为+＝，所以w＝＝＝4.

又因为函数图象过点(－，2)，

所以2＝2sin[4×(－)+φ]．

∵0＜φ＜π，

解得：φ＝，所以(w，φ)＝(4，)．

8．(2009·天津，7)已知函数f(x)＝sin(wx+)(x∈R，w＞0)的最小正周期为π，为了得到函数g(x)＝coswx的图象，只要将y＝f(x)的图象　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．向左平移个单位长度

B．向右平移个单位长度

C．向左平移个单位长度

D．向右平移个单位长度

答案：A

解析：∵f(x)＝sin(wx+)(x∈R，w＞0)的最小正周期为π，

∴＝π，故w＝2.又f(x)＝sin(2x+)

向左平移\f(π8g(x)＝sin[2(x+)+]＝sin(2x+)＝cos2x，故选A.

7．(2009·重庆，6)下列关系中正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．sin11°＜cos10°＜sin168°

B．sin168°＜sin11°＜cos10°

C．sin11°＜sin168°＜cos10°

D．sin168°＜cos10°＜sin11°

答案：C

解析：∵sin11°＝cos79°，sin168°＝cos78°，又∵y＝cosx在[0，]上单调递减，79°＞78°＞10°，∴cos10°＞sin168°＞sin11°，故选C.

6．下列各式中，值为的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．sin15°cos15°　 B．cos²－sin²

C.　 D.

答案：D

解析：由tan45°＝，知选D.

5．(2009·广东，9)函数y＝2cos²(x－)－1是　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．最小正周期为π的奇函数

B．最小正周期为π的偶函数

C．最小正周期为的奇函数

D．最小正周期为的偶函数

答案：A

解析：由y＝2cos²(x－)－1

＝cos(2x－)＝sin2x，

∴T＝π，且为奇函数，故选A.

4．(2009·辽宁，8)已知tanθ＝2，则sin²θ+sinθcosθ－2cos²θ＝　　　　　　　　　　　　　 (　)

A．－　 　　　　　　 B.　 　　　　　　 C．－　 　　　　　　　 D.

答案：D

解析：sin²θ+sinθcosθ－2cos²θ

＝

＝

＝＝.故选D.