
题目列表(包括答案和解析)
4.转化与化归的思想
在解决恒成立及复合函数等问题时,往往可以把问题转化为指数函数、对数函数、二次函数、幂函数等我们熟悉的函数去研究,将复杂的问题分解、归结为简单问题.
例4 已知函数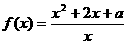 ,
,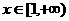 ,若对任意
,若对任意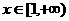 ,
,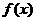 >0恒成立,试求实数
>0恒成立,试求实数 的取值范围.
的取值范围.
解:在区间[1,+ )上,
)上,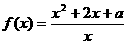 >0恒成立
>0恒成立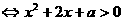 恒成立.
恒成立.
设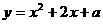 ,
,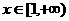
∵ 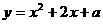 =
=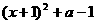 递增,
递增,
∴当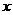 =1时,
=1时,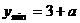 ,当且仅当
,当且仅当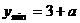 >0时,函数
>0时,函数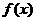 >0恒成立.
>0恒成立.
故 >-3
>-3
3.分类讨论的思想
在函数这一部分经常涉及到分类讨论的情形,特别是含参数的二次函数在部分区间上的最值问题,含参数的函数单调性的研究及应用等问题中,一般需用分类讨论的思想方法.
例3 已知函数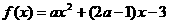 在区间[-
在区间[-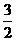 ,2]上的最大值为1,求实数
,2]上的最大值为1,求实数 的值.
的值.
解: =0时,
=0时,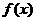 =-
=-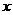 -3,
-3,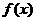 在[-
在[-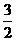 ,2]上不能取得1,故
,2]上不能取得1,故
 0.
0.
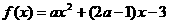 (
(
 0)的对称轴方程为
0)的对称轴方程为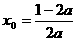
(1)令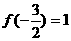 ,解得
,解得 =-
=-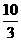 ,此时
,此时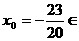 [-
[-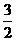 ,2]
,2]
∵  <0,
<0,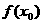 最大,所以
最大,所以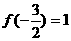 不合适.
不合适.
(2)令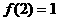 ,解得
,解得 =
=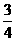 ,此时
,此时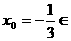 [-
[-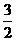 ,2]
,2]
∵  =
=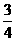 >0, ∴
>0, ∴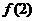 最大,合适.
最大,合适.
(3)令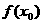 =1,解得
=1,解得 =
=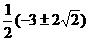 ,验证后知只有
,验证后知只有 =
=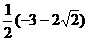 才合适.
才合适.
综上所述, =
=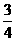 ,或
,或 =
=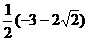 .
.
2.数形结合的思想方法
函数的图像直观地显示函数的性质,借助于图像来研究、解决有关函数的问题是数形结合应用的一个重要方面.在解不等式、判断方程是否有解、解的个数及二次方程根的分布问题时,我们往往构造函数,利用函数的图像解题.
例2 方程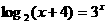 的解的个数是( )
的解的个数是( )
A.0个 B.1个 C.2个 D.3个
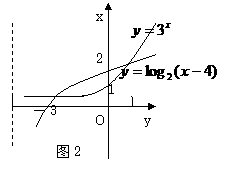 解:在同一坐标系画出函数
解:在同一坐标系画出函数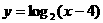
及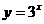 的图像,
的图像,
如图2,他们的图像有两个交点.故选C.
1.对应的思想
在本章中,映射是一种对应,函数是一种对应,并且函数是按照某种对应关系建立的从定义域到值域的映射,因此函数的定义域、对应关系确定以后,值域就确定了,在解题中,一定注意函数定义域.
例1 已知集合M={1,2,3},N={4,5},函数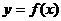 以M为定义域,以N为值域,则这样的函数共有------
以M为定义域,以N为值域,则这样的函数共有------
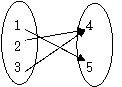
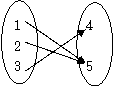
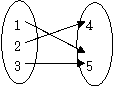
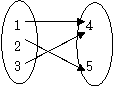
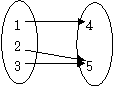
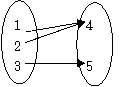 解:
解:
图1
由图可知,这样的函数共有6个.
5.正比例函数模型
例5 一个圆柱形容器的底面直径为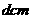 ,高度为
,高度为 ,现以每秒
,现以每秒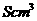 的速度向容器内注入某种溶液,求容器内的溶液高度
的速度向容器内注入某种溶液,求容器内的溶液高度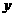 与注入时间
与注入时间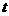
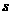 的函数关系式及其定义域。
的函数关系式及其定义域。
分析:圆柱体的容积即是圆柱体的体积=底面积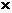 高,可变形成另一种形式为高=
高,可变形成另一种形式为高= 。
。
解析:依题意,容器内溶液每秒升高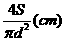 ,得函数关系为
,得函数关系为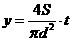 ,
,
注满容器所需时间为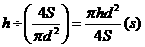 ,函数的定义域为
,函数的定义域为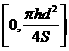 。
。
评注:正比例函数模型是函数应用问题中常用的数学模型,应熟练掌握。
4.一次函数模型
例4 某家报刊销售点从报社买进报纸的价格是每份0.35元,卖出的价格是每份0.50元,卖不掉的报纸还可以每份0.08元的价格退回报社。在一个月(30天)里,有20天每天可以卖出400份,其余10天每天只能卖出250份。设每天从报社买进报纸的数量相同,则应该每天从报社买进多少份,才能使每月所获的利润最大?并计算该销售点一个月最多可赚得多少元?
分析:每月赚得的钱=卖报收入的总价-付给报社的总价。而收入的总数分为三部分,一是在可卖出400份的20天里,收入为0.5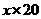 ;二是在可卖出250份的10天里,在
;二是在可卖出250份的10天里,在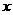 份报纸中,有250份报纸可卖出,收入为0.5
份报纸中,有250份报纸可卖出,收入为0.5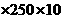 ;三是没有卖掉的(
;三是没有卖掉的(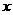 -250)份报纸可退回报社,报社付出
-250)份报纸可退回报社,报社付出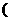
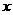 -250
-250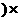 0.08
0.08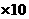 的钱。
的钱。
解析:设每天应从报社买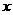 份,易知
份,易知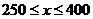 ,
,
设每月赚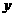 元,则
元,则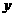 =0.5
=0.5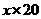 +0.5
+0.5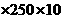 +
+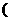
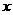 -250
-250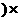 0.08
0.08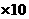 -0.35
-0.35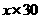
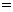 0.3
0.3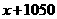 ,
,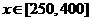 。
。
因为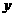
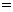 0.3
0.3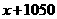 是定义域上的增函数,
是定义域上的增函数,
所以当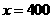 时,
时,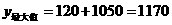 (元)。
(元)。
故每天应从报社买进400份报纸,获得利润最大,每月可赚1170元。
评注:函数式的定义域不能漏掉。
3.二次函数模型
例4 某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数:
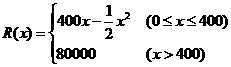 ,其中
,其中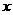 是仪器的月产量。
是仪器的月产量。
(1)将利润表示为月产量的函数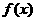 ;
;
(2)当月产量为何值时,公司所或利润最大?最大利润为多少元?
(总收益=总成本+利润)
分析:由已知总收益=总成本+利润,知道利润=总收益-总成本,由于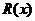 是分段函数,所以
是分段函数,所以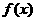 也要分段求出。分别求出
也要分段求出。分别求出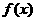 在各段中的最大值,通过比较,就能确定
在各段中的最大值,通过比较,就能确定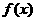 的最大值。
的最大值。
解析:(1)设月产量为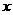 台,则总成本为20000+100
台,则总成本为20000+100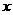 ,从而
,从而
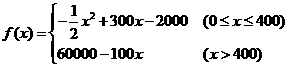 。
。
(2)当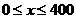 时,
时,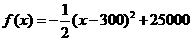 ,
,
∴当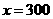 时,有最大值25000;
时,有最大值25000;
当 时,
时, 是减函数,
是减函数,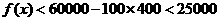 。
。
故当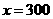 时,
时,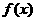 的最大值为25000元。
的最大值为25000元。
评注:该例中的“利润=总收益-总成本”是解题的关键所在。
2.对数模型
例2
我们都处于有声世界之中,不同的场合人们对音量会有不同的要求,音量大小的单位是分贝(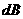 ),对于一个强度为
),对于一个强度为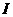 的声波,分贝的定义是:
的声波,分贝的定义是:
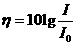 ,这里
,这里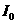 是人耳能听到的声音的最低声波强度,
是人耳能听到的声音的最低声波强度,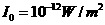 ,当
,当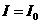 时,
时,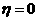 ,即
,即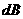 =0。
=0。
(1)如果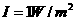 ,求相应的分贝值;
,求相应的分贝值;
(2)70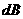 时的声音强度
时的声音强度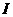 是60
是60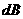 时声音强度
时声音强度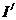 的多少倍?
的多少倍?
分析:已知的等量关系是解决函数应用问题的依据。
解析:(1)将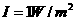 代入
代入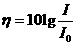 得
得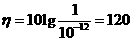 (
(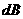 );
);
(2)当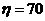 时,解得
时,解得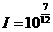 ,当
,当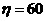 时,解得
时,解得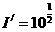 ,
,
∴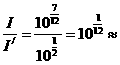 1.2,
1.2,
故70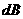 时的声音强度
时的声音强度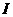 是60
是60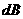 时声音强度
时声音强度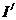 的1.2倍。
的1.2倍。
评注:在平时的学习过程中,熟练掌握一些基本的数学模型,有助于提高我们解决实际问题的能力。
1.指数模型
例1 某公司拟投资100万元,有两种获利的可能可供选择:一种是年利润10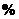 ,按单利计算,5年后收回本金和利息;另一种是按年利率9
,按单利计算,5年后收回本金和利息;另一种是按年利率9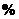 ,按每一年复利一次计算,5年后收回本金和利息,哪一种投资更有利?这种投资比另一种投资5年可多得利息多少元?
,按每一年复利一次计算,5年后收回本金和利息,哪一种投资更有利?这种投资比另一种投资5年可多得利息多少元?
分析:本例可先按单利和复利分别计算5年后的本息和,再通过比较即可。
解析:依题意,本金100万元,年利率10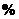 ,按单利计算,5年后的本息和是
,按单利计算,5年后的本息和是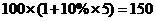 (万元);
(万元);
本金100万元,年利率9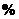 ,按每年复利一次计算,5年后的本息和是
,按每年复利一次计算,5年后的本息和是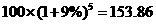 (万元);
(万元);
由此可见,按年利率9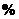 每年复利一次计算要比年利率10
每年复利一次计算要比年利率10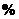 的单利计算更有利,5年后多得利息3.86万元。
的单利计算更有利,5年后多得利息3.86万元。
评注:单利是正比例函数,而复利是指数函数模型,可见复利计算得到的利息要多。
15.设O为直径等于a的圆上一点,过 O点任意作直线交圆于P点,在射线OP上取一点M,使 =a,当 P点在圆上移动一周时,求相应的点M的轨迹方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com