
题目列表(包括答案和解析)
4.(2009·成化高级中学高三期中考试)已知函数f(x)=ax+b(0≤x≤1),则“a+2b>0” “是f(x)>0”恒成立的
条件.(填“充分不必要”、“必要不充分”、“充分必要”、“既不充分也不必要”之一)
答案 必要不充分
3.“x>1”是“x2>x”的 条件.
? 答案 充分不必要
2.(2008·重庆理,2)设m,n是整数,则“m,n均为偶数”是“m+n是偶数”的 条件.
答案 充分不必要
1.下列命题:①5>4或4>5;②9≥3;③命题“若a>b,则a+c>b+c”的否命题;④命题“矩形的两条对角线相等”的逆命题.其中假命题的个数为 .
答案 1
12.设α、β是方程x2-ax+b=0的两个根,试分析a>2且b>1是两根α、β均大于1的什么条件?
解 令p:a>2,且b>1;q:α>1,且β>1,易知α+β=a,αβ=b.
①若a>2,且b>1,即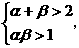 不能推出α>1且β>1.
不能推出α>1且β>1.
可举反例:若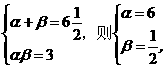 所以由p推不出q;
所以由p推不出q;
②若α>1,且β>1,则α+β>1+1=2,αβ>1.所以由q可推出p.综合知p是q的必要不充分条件,也即a>2,且b>1是两根α、β均大于1的必要不充分条件.
11. a,b,c为实数,且a=b+c+1.证明:两个一元二次方程x2+x+b=0,x2+ax+c=0中至少有一个方程有两个不相等的实数根.
证明 假设两个方程都没有两个不等的实数根,则
?Δ1=1-4b≤0,Δ2=a2-4c≤0, ∴Δ1+Δ2=1-4b+a2-4c≤0.
∵a=b+c+1,∴b+c=a-1. ∴1-4(a-1)+a2≤0,
即a2-4a+5≤0. 但是a2-4a+5=(a-2)2+1>0,故矛盾.
所以假设不成立,原命题正确,即两个方程中至少有一个方程有两个不相等的实数根.
10. 已知x,y∈R.
求证:|x+y|=|x|+|y|成立的充要条件是xy≥0.
证明(充分性)
若xy≥0,则x,y至少有一个为0或同号.∴|x+y|=|x|+|y|一定成立.
(必要性) 若|x+y|=|x|+|y|,则(x+y)2=(|x|+|y|)2, x2+2xy+y2=x2+2|xy|+y2,
∴xy=|xy|,∴xy≥0. 综上,命题得证.
9. 求关于x的方程x2-mx+3m-2=0的两根均大于1的充要条件.
解 设方程的两根分别为x1、x2,则原方程有两个大于1的根的充要条件是
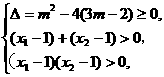 即
即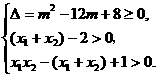
又∵x1+x2=m,x1x2=3m-2, ∴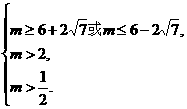 故所求的充要条件为m≥6+2
故所求的充要条件为m≥6+2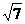 .
.
8.设A=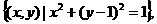 B
B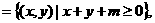 则使A
则使A B成立的实数m的取值范围是 .
B成立的实数m的取值范围是 .
答案 m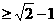
7.设集合A=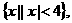 B
B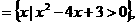 则集合
则集合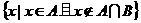 =
.
=
.
答案 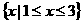
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com