12．已知圆M过两点C(1，－1)，D(－1,1)，且圆心M在x+y－2＝0上．

(1)求圆M的方程；

(2)设P是直线3x+4y+8＝0上的动点，PA、PB是圆M的两条切线，A、B为切点，求四边形PAMB面积的最小值．

解：(1)设圆M的方程为：(x－a)²+(y－b)²＝r²(r>0)．

根据题意，得

解得a＝b＝1，r＝2，

故所求圆M的方程为(x－1)²+(y－1)²＝4.

(2)因为四边形PAMB的面积S＝S_△PAM+S_△PBM＝|AM|·|PA|+|BM|·|PB|，

又|AM|＝|BM|＝2，|PA|＝|PB|，

所以S＝2|PA|，

而|PA|＝＝，

即S＝2.

因此要求S的最小值，只需求|PM|的最小值即可，

即在直线3x+4y+8＝0上找一点P，使得|PM|的值最小，

所以|PM|_min＝＝3，

所以四边形PAMB面积的最小值为S＝2＝2＝2.

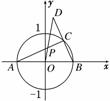
11.如图，已知点A(－1,0)与点B(1,0)，C是圆x²+y²＝1上的动点，连结BC并延长至D，使得|CD|＝|BC|，求AC与OD的交点P的轨迹方程．

解：设动点P(x，y)，由题意可知P是△ABD的重心．

由A(－1,0)，B(1,0)，令动点C(x₀，y₀)，则D(2x₀－1,2y₀)，由重心坐标公式：

则代入x²+y²＝1，整理得

所求轨迹方程为(x+)²+y²＝(y≠0)．

10．已知直线l₁：4x+y＝0，直线l₂：x+y－1＝0以及l₂上一点P(3，－2)．求圆心C在l₁上且与直线l₂相切于点P的圆的方程．

解：设圆心为C(a，b)，半径为r，依题意，得b＝－4a.

又PC⊥l₂，直线l₂的斜率k₂＝－1，

∴过P，C两点的直线的斜率k_PC＝＝1，

解得a＝1，b＝－4，r＝|PC|＝2.

故所求圆的方程为(x－1)²+(y+4)²＝8.

9．若圆的方程为x²+y²+kx+2y+k²＝0，则当圆的面积最大时，圆心为________．

解析：方程为x²+y²+kx+2y+k²＝0

化为标准方程为(x+)²+(y+1)²＝1－

∵r²＝1－≤1，∴k＝0时r最大．

此时圆心为(0，－1)．

答案：(0，－1)

8．圆C的半径为1，圆心在第一象限，与y轴相切，与x轴相交于点A、B，若|AB|＝，则该圆的标准方程是__________．

解析：根据|AB|＝，可得圆心到x轴的距离为，故圆心坐标为(1，)，故所求圆的标准方程为(x－1)²+(y－)²＝1.

答案：(x－1)²+(y－)²＝1

7．若圆x²+y²－ax+2y+1＝0与圆x²+y²＝1关于直线y＝x－1对称，过点C(－a，a)的圆P与y轴相切，则圆心P的轨迹方程为________．

解析：由圆x²+y²－ax+2y+1＝0与圆x²+y²＝1关于直线y＝x－1对称可知两圆半径相等且两圆圆心连线的中点在直线y＝x－1上，故可得a＝2，即点C(－2,2)，所以过点C(－2,2)且与y轴相切的圆P的圆心的轨迹方程为(x+2)²+(y－2)²＝x²，整理即得y²+4x－4y+8＝0.

答案：y²+4x－4y+8＝0

6．(2010·西安模拟)已知圆的方程为x²+y²－6x－8y＝0，设该圆中过点M(3,5)的最长弦、最短弦分别为AC、BD，则以点A、B、C、D为顶点的四边形ABCD的面积为(　)

A．10　 　　　　　　 B．20

C．30　 　　　　　　 D．40

解析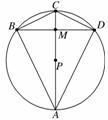：将圆的方程化成标准形式得(x－3)²+(y－4)²＝25，所以圆心为P(3,4)，半径r＝5.而|MP|＝＝1<5，所以点M(3,5)在圆内，故当过点M的弦经过圆心时最长，此时|AC|＝2r＝10，当弦BD与MP垂直时，弦BD的长度最小，此时|BD|＝2＝2＝4.又因为AC⊥BD，所以四边形ABCD的面积为S＝|AC|×|BD|＝×10×4＝20.

答案：B

5．圆心在抛物线y²＝2x(y>0)上，并且与抛物线的准线及x轴都相切的圆的方程是(　)

A．x²+y²－x－2y－＝0　 　　　　　　　　　　 B．x²+y²+x－2y+1＝0

C．x²+y²－x－2y+1＝0　 　　　　　　　　　　 D．x²+y²－x－2y+＝0

解析：抛物线y²＝2x(y>0)的准线为x＝－，圆与抛物线的准线及x轴都相切，则圆心在直线y＝x+(y>0)上，与y²＝2x(y>0)联立可得圆心的坐标为(，1)，半径为1，则方程为(x－)²+(y－1)²＝1，化简得x²+y²－x－2y+＝0.

答案：D

4．圆x²+y²+2x－4y+1＝0关于直线2ax－by+2＝0(a，b∈R)对称，则ab的取值范围是(　)

A．(－∞，]　 　　　 B．(0，)

C．(－，0) 　　　　　　　　 　D．(－∞，)

解析：由题可知直线2ax－by+2＝0过圆心(－1,2)，故可得a+b＝1，又因ab≤()²＝.

答案：A

3．(2011·青岛二中期末)若圆C的半径为1，圆心在第一象限，且与直线4x－3y＝0和x轴都相切，则该圆的标准方程是(　)

A．(x－3)²+²＝1　 　　　　　　　　 B．(x－2)²+(y－1)²＝1

C．(x－1)²+(y－3)²＝1　 　　　　　　　 D.²+(y－1)²＝1

解析：依题意设圆心C(a,1)(a>0)，由圆C与直线4x－3y＝0相切，得＝1，解得a＝2，则圆C的标准方程是(x－2)²+(y－1)²＝1.

答案：B