
题目列表(包括答案和解析)
3.已知A、B、C的坐标分别为A(4,0),B(0,4),C(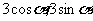 ).若
).若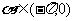 ,且
,且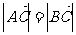 ,求角
,求角 的大小;
的大小;
解析:(Ⅰ)由已知得:
则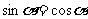 因为
因为
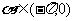
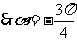
2. 已知向量a=(3sinα,cosα),b=(2sinα,
5sinα-4cosα),α∈(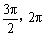 ),且a⊥b. 求tanα的值;
),且a⊥b. 求tanα的值;
解:(1)∵a⊥b,∴a·b=0.而a=(3sinα,cosα),b=(2sinα, 5sinα-4cosα),
故a·b=6sin2α+5sinαcosα-4cos2α=0.
由于cosα≠0,∴6tan2α+5tanα-4 =0.解之,得tanα=-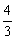 ,或tanα=
,或tanα=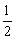 .
.
∵α∈(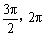 ),tanα<0,故tanα=
),tanα<0,故tanα=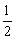 (舍去).∴tanα=-
(舍去).∴tanα=-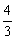 .
.
题型3.给式求角
例4.(广东省揭阳市2008年第一次模拟考试)已知:向量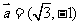 ,
,
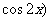 ,函数
,函数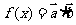 ,若
,若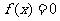 且
且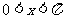
 ,求
,求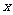 的值;
的值;
[解题思路]先由向量运算得出三角函数间的关系,再进一步处理。
解析:∵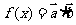 =
=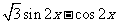 -
-
由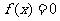 得
得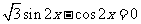 即
即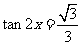
∵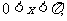
 ∴
∴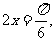 或
或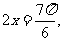
∴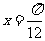 或
或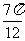 -
-
[名师指引]给式求角问题可考虑先求出一种三角函数值,再精确估计角的范围再定角。
例5.(2007·四川 )已知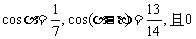 <
< <
<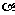 <
<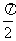 ,
,
(Ⅰ)求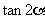 的值.(Ⅱ)求
的值.(Ⅱ)求 .
.
[解题思路]由同角关系求出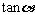 再求
再求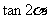 ;又
;又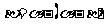 结合角
结合角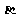 的范围定角。
的范围定角。
[解析](Ⅰ)由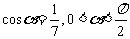 ,得
,得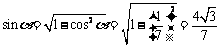
∴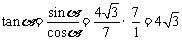 ,于是
,于是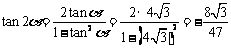
(Ⅱ)由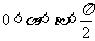 ,得
,得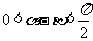
又∵ ,∴
,∴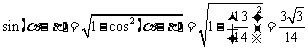
由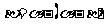 得:
得: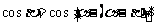
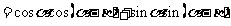
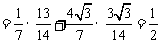 ,所以
,所以
[名师指引]本题考察三角恒等变形的主要基本公式、三角函数值的符号,已知三角函数值求角以及计算能力。
[新题导练]
1. 已知函数f(x)=2sinxcosx+cos2x.
(Ⅰ)求f (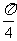 )的值;
)的值;
(Ⅱ)设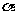 ∈(0,
∈(0,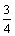
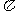 ),f (
),f (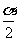 )=
)=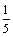 ,求cos2
,求cos2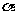 的值.
的值.
解析:(Ⅰ)∵f(x)=sin2x+cos2x,∴f(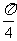 )=sin
)=sin +cos
+cos =1
=1
(Ⅱ)∵f( )=sinα+cosα=
)=sinα+cosα=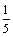 ,∴1+sin2α=
,∴1+sin2α=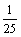 , sin2α=
, sin2α=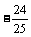 ,
,
∴cos2α=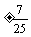 ∵α∈(0,
∵α∈(0,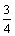 π)∴2α∈(π,
π)∴2α∈(π,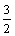 π) ∴cos2α<0.
π) ∴cos2α<0.
故cos2α=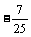
2.(08海南省)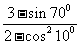 =()
=()
A. 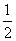 B.
B.  C.
2 D.
C.
2 D. 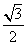
[解析]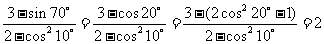 ,选C。
,选C。
答案:C
题型2给式求值
[例2] (惠州市2009届高三第三次调研考试数学试题)已知 .
.
(1)求 的值;
的值;
(2)求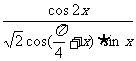 的值.
的值.
[解题思路]第(1)问注意到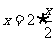 ,第(2)问对三角式化为
,第(2)问对三角式化为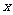 的表达式.
的表达式.
解析:(1)由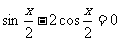 ,
, 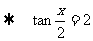 ,
,
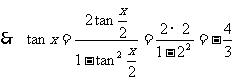 .
.
(2) 原式= 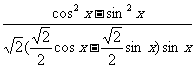
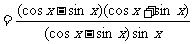

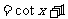
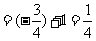 .
.
[名师指引]给式求值一般从分析角的关系入手.
例3. (福建省师大附中2008年高三上期期末考试)
设向量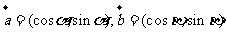 ,
,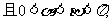 若
若 ,
,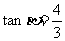 ,求
,求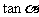 的值。
的值。
[解题思路]先进行向量计算,再找角的关系.
解析:

[名师指引]三角与向量是近几年高考的热门题型,这类题往往是先进行向量运算,再进行三角变换
[新题导练]
1. (tan5°-cot5°)·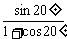
解:原式=
3.重难点:通过审题分析已知条件和待求结论之间角的差异,建立联系,使问题获解。
(1)三角变换的基本思路是“变角、变名、变式”
问题1: (07江苏)若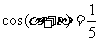 ,
,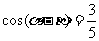 ,则
,则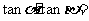 _____.
_____.
点拨:已知条件中的角是 ,待求式中的角是
,待求式中的角是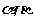 ,故只需将条件展开,再由同角关系式来处理。由
,故只需将条件展开,再由同角关系式来处理。由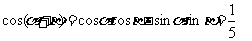
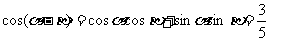
求出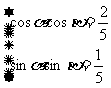

(2) 处理三角式的化简、求值和证明问题的基本原则是“见平方就降次,见切割就化弦,充分利用同角关系式,关注符号定象限,象限定符号的特征”。
问题2:已知 ,
,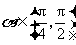 .求
.求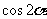 和
和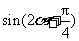 的值.
的值.
点拨:本题考查同角三角函数关系、两角和公式、倍角公式等基础知识,考查基本运算能力。先将切化弦,再寻找角之间的关系。
由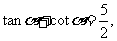 得
得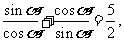 则
则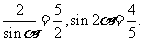
因为 所以
所以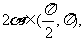
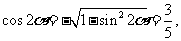

★热 点 考 点 题 型 探 析
考点1: 三角求值题的处理
题型1.给角求值问题
[例1] (山东省聊城一中2008-2009学年度上学期高三年级期末综合测试)
不查表求值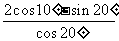 =
.
=
.
[解题思路]要注意到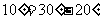 ,然后用公式展开.
,然后用公式展开.
[解析]原式 = 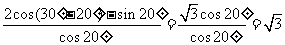 .
.
[名师指引]给角求值问题一般考虑通过变角凑出特殊解且设法将非特殊角抵消或约去,注意公式的顺用、逆用和变形用.
[新题导练]
2.难点:确定三角变换的方向及三角公式的合理运用.
1.重点:掌握利用三角恒等变换处理三角式化简,求值与证明等问题。
2. 同角正余弦化积公式
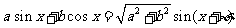 ,其中
,其中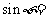
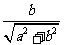 ;
;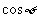 =
=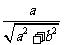
★重 难 点 突 破
1. 升降幂公式:

 ;
;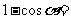

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com