
题目列表(包括答案和解析)
13.对于任意的两个实数对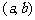 和
和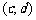 ,规定:
,规定: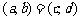 ,当且仅当
,当且仅当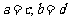 ;运算“
;运算“ ”为:
”为: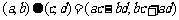 ;运算“
;运算“ ”为:
”为: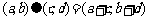 ,设
,设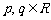 ,若
,若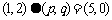 ,则
,则 ………( )
………( )
A.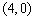 B.
B.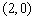 C.
C.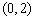 D.
D.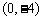
解:由题意,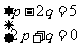 ,解得
,解得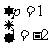 ,所以正确答案为(B).
,所以正确答案为(B).
点评:实际上,本题所定义的实数对的两种运算就是复数的乘法与加法运算.我们可以把该题还原为:已知复数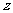 满足
满足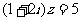 ,则
,则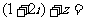 _____________.
_____________.
★抢分频道★
基础巩固训练
12. (2008惠州调研二)为确保信息安全,信息需加密传输,发送方由明文 密文(加密),接受方由密文
密文(加密),接受方由密文 明文(解密),已知加密规则为:明文
明文(解密),已知加密规则为:明文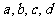 对应密文
对应密文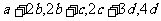 ,例如,明文
,例如,明文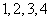 对应密文
对应密文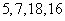 .当接受方收到密文
.当接受方收到密文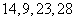 时,则解密得到的明文为( ).
时,则解密得到的明文为( ).
A. 4,6,1,7 B. 7,6,1,4 C. 6,4,1,7 D. 1,6,4,7
[解析] 由 得
得 ,选C
,选C
11. (2008深圳二模文)一个质点从
(2008深圳二模文)一个质点从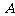 出发依次沿图中线段到达
出发依次沿图中线段到达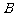 、
、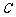 、
、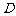 、
、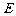 、
、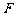 、
、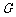 、
、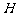 、
、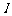 、
、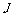 各点,最后又回到
各点,最后又回到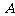 (如图所示),其中:
(如图所示),其中: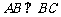 ,
,
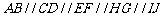 ,
,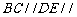
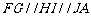 .
.
欲知此质点所走路程,至少需要测量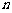 条线段的长度,
条线段的长度,
则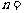 ( B )
( B )
A.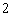 B.
B.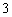 C.
C.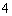 D.
D.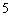
[解析]只需测量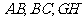 3条线段的长
3条线段的长
10. (2008珠海质检理)定义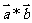 是向量a和b的“向量积”,它的长度
是向量a和b的“向量积”,它的长度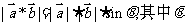 为向量a和b的夹角,若
为向量a和b的夹角,若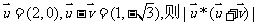 =
.
=
.
[解析]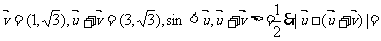
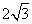
9.已知等差数列的定义为:在一个数列中,从第二项起,如果每一项与它的前一项的差都为同一个常数,那么这个数叫做等差数列,这个常数叫做该数列的公差.
类比等差数列的定义给出“等和数列”的定义: ;
已知数列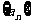 是等和数列,且
是等和数列,且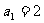 ,公和为
,公和为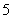 ,那么
,那么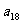 的值为____________.这个数列的前
的值为____________.这个数列的前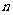 项和
项和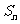 的计算公式为_____________________________________.
的计算公式为_____________________________________.
[解析]在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数叫做等和数列,这个常数叫做该数列的公和;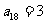 ;
;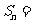

考点2 演绎推理
题型:利用“三段论”进行推理
[例1 ] (07启东中学模拟)某校对文明班的评选设计了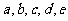 五个方面的多元评价指标,并通过经验公式样
五个方面的多元评价指标,并通过经验公式样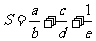 来计算各班的综合得分,S的值越高则评价效果越好,若某班在自测过程中各项指标显示出
来计算各班的综合得分,S的值越高则评价效果越好,若某班在自测过程中各项指标显示出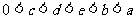 ,则下阶段要把其中一个指标的值增加1个单位,而使得S的值增加最多,那么该指标应为
.(填入
,则下阶段要把其中一个指标的值增加1个单位,而使得S的值增加最多,那么该指标应为
.(填入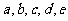 中的某个字母)
中的某个字母)
[解题思路]从分式的性质中寻找S值的变化规律
[解析] 因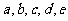 都为正数,故分子越大或分母越小时, S的值越大,而在分子都增加1的前提下,分母越小时,S的值增长越多,
都为正数,故分子越大或分母越小时, S的值越大,而在分子都增加1的前提下,分母越小时,S的值增长越多,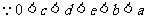 ,所以c增大1个单位会使得S的值增加最多
,所以c增大1个单位会使得S的值增加最多
[名师指引]此题的大前提是隐含的,需要经过思考才能得到
[例2 ] (03上海)已知集合M是满足下列性质的函数f(x)的全体:存在非零常数T,对任意x∈R,有f(x+T)=T f(x)成立.
(1)函数f(x)= x 是否属于集合M?说明理由;
(2)设函数f(x)=ax(a>0,且a≠1)的图象与y=x的图象有公共点,证明: f(x)=ax∈M;
(3)若函数f(x)=sinkx∈M ,求实数k的取值范围.
[解题思路]函数f(x)是否属于集合M,要看f(x)是否满足集合M的“定义”,
[解](1)对于非零常数T,f(x+T)=x+T, Tf(x)=Tx. 因为对任意x∈R,x+T= Tx不能恒成立,所以f(x)=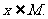
(2)因为函数f(x)=ax(a>0且a≠1)的图象与函数y=x的图象有公共点,
所以方程组: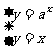 有解,消去y得ax=x,
有解,消去y得ax=x,
显然x=0不是方程ax=x的解,所以存在非零常数T,使aT=T.
于是对于f(x)=ax有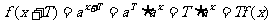 故f(x)=ax∈M.
故f(x)=ax∈M.
(3)当k=0时,f(x)=0,显然f(x)=0∈M.
当k≠0时,因为f(x)=sinkx∈M,所以存在非零常数T,对任意x∈R,有
f(x+T)=T f(x)成立,即sin(kx+kT)=Tsinkx .
因为k≠0,且x∈R,所以kx∈R,kx+kT∈R,
于是sinkx ∈[-1,1],sin(kx+kT) ∈[-1,1],
故要使sin(kx+kT)=Tsinkx .成立,
只有T= ,当T=1时,sin(kx+k)=sinkx
成立,则k=2mπ, m∈Z .
,当T=1时,sin(kx+k)=sinkx
成立,则k=2mπ, m∈Z .
当T=-1时,sin(kx-k)=-sinkx 成立,
即sin(kx-k+π)= sinkx 成立,
则-k+π=2mπ, m∈Z ,即k=-2(m-1) π, m∈Z .
实数k的取值范围是{k|k= mπ, m∈Z}
[名师指引]学会紧扣“定义”解题
[新题导练]
8. 对于一元二次方程,有以下正确命题:如果系数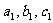 和
和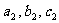 都是非零实数,方程
都是非零实数,方程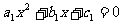 和
和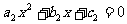 在复数集上的解集分别是
在复数集上的解集分别是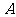 和
和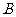 ,则“
,则“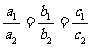 ”是“
”是“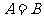 ”的充分必要条件.
”的充分必要条件.
试对两个一元二次不等式的解集写出类似的结果,并加以证明.
解:(3)如果系数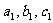 和
和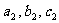 都是非零实数,不等式
都是非零实数,不等式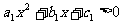 和
和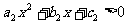 的解集分别是
的解集分别是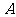 和
和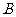 ,则“
,则“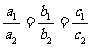 ”是“
”是“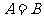 ”的既不充分也不必要条件.可以举反例加以说明.
”的既不充分也不必要条件.可以举反例加以说明.
7. (2008届广东省东莞市高三理科数学高考模拟题(二))
在平面直角坐标系中,直线一般方程为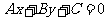 ,圆心在
,圆心在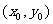 的圆的一般方程为
的圆的一般方程为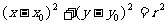 ;则类似的,在空间直角坐标系中,平面的一般方程为________________,球心在
;则类似的,在空间直角坐标系中,平面的一般方程为________________,球心在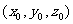 的球的一般方程为_______________________.
的球的一般方程为_______________________.
[解析]  ;
;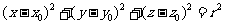
6. (2008梅州一模)已知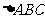 的三边长为
的三边长为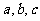 ,内切圆半径为
,内切圆半径为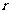 (用
(用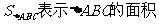 ),则
),则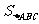
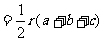 ;类比这一结论有:若三棱锥
;类比这一结论有:若三棱锥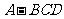 的内切球半径为
的内切球半径为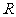 ,则三棱锥体积
,则三棱锥体积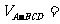
[解析] 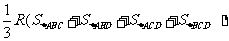
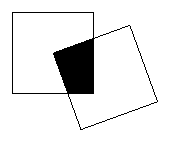
5. (2008深圳二模文)现有一个关于平面图形的命题:如图,同一个平面内有两个边长都是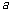 的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为
的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为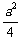 .类比到空间,有两个棱长均为
.类比到空间,有两个棱长均为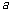 的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 .
的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 .
[解析]解法的类比(特殊化),易得两个正方体重叠部分的体积为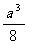
4. (2008揭阳一模)
设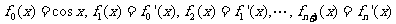 ,
,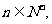
则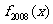 =( )
=( )
A. 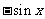 B.
B. 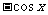 C.
C. 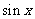 D.
D. 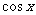
[解析]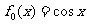 ,
,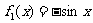 ,
,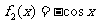 ,
,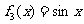 ,
,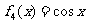 ,
,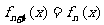 ,
,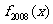 =
=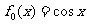
题型2 用类比推理猜想新的命题
[例1
] (2008韶关调研)已知正三角形内切圆的半径是高的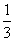 ,把这个结论推广到空间正四面体,类似的结论是______.
,把这个结论推广到空间正四面体,类似的结论是______.
[解题思路]从方法的类比入手
[解析]原问题的解法为等面积法,即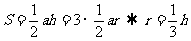 ,类比问题的解法应为等体积法,
,类比问题的解法应为等体积法, 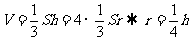 即正四面体的内切球的半径是高
即正四面体的内切球的半径是高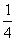
[名师指引](1)不仅要注意形式的类比,还要注意方法的类比
(2)类比推理常见的情形有:平面向空间类比;低维向高维类比;等差数列与等比数列类比;实数集的性质向复数集的性质类比;圆锥曲线间的类比等
[例2
] 在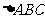 中,若
中,若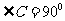 ,则
,则 ,用类比的方法,猜想三棱锥的类似性质,并证明你的猜想
,用类比的方法,猜想三棱锥的类似性质,并证明你的猜想
[解题思路]考虑两条直角边互相垂直如何类比到空间以及两条直角边与斜边所成的角如何类比到空间
[解析]由平面类比到空间,有如下猜想:“在三棱锥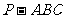 中,三个侧面
中,三个侧面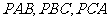 两两垂直,且与底面所成的角分别为
两两垂直,且与底面所成的角分别为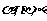 ,则
,则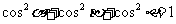 ”
”
证明:设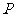 在平面
在平面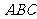 的射影为
的射影为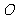 ,延长
,延长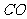 交
交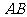 于
于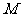 ,记
,记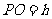
由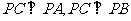 得
得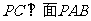 ,从而
,从而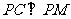 ,又
,又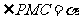
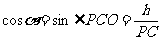 ,
,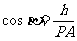 ,
,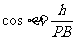
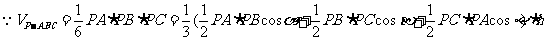
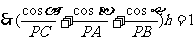 即
即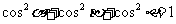
[名师指引](1)找两类对象的对应元素,如:三角形对应三棱锥,圆对应球,面积对应体积,平面上的角对应空间角等等;(2)找对应元素的对应关系,如:两条边(直线)垂直对应线面垂直或面面垂直,边相等对应面积相等
 [新题导练]
[新题导练]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com