
题目列表(包括答案和解析)
10.已知正四棱锥S-ABCD的侧棱长与底面边长都相等,E是SB的中点,
则AE、SD所成的角的余弦值为 .
9.在棱长为1的正方体ABCD-A1B1C1D1中,E、F分别为棱AA1、BB1的中点,G为棱A1B1上的一点,且A1G=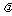 (0≤
(0≤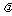 ≤1),则点G到平面D1EF的距离为
.
≤1),则点G到平面D1EF的距离为
.
8.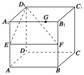 矩形ABCD的两边AB=3,AD=4,PA⊥平面ABCD,且PA=
矩形ABCD的两边AB=3,AD=4,PA⊥平面ABCD,且PA=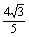 ,则二面角A-BD-P的度数为
.
,则二面角A-BD-P的度数为
.
7.正方体的全面积为24,球O与正方体的各棱均相切,球O的体积是 .
6.关于直线m、n与平面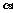 、
、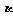 ,有下列四个命题:
,有下列四个命题:
①m∥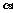 ,n∥
,n∥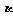 且
且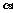 ∥
∥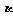 ,则m∥n;②m⊥
,则m∥n;②m⊥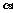 ,n⊥
,n⊥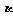 且
且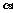 ⊥
⊥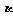 ,则m⊥n;
,则m⊥n;
③m⊥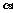 ,n∥
,n∥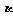 且
且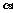 ∥
∥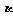 ,则m⊥n;④m∥
,则m⊥n;④m∥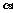 ,n⊥
,n⊥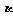 且
且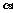 ⊥
⊥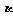 ,则m∥n.
,则m∥n.
其中真命题的序号是 .
5.把半径为1的四个球垒成两层放在桌上,下层三个,上层一个,两两相切,则上层小球的球心到桌面的距离是 .
4.如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则AC1与
平面A1B1C1D1所成角的正弦值为 .
3.如下图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的全面积为 .


2.过球的一条半径的中点,作垂直于该半径的平面,则所得截面的面积与球的表面积
的比为 .
1.设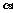 、
、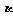 、
、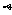 是三个不重合的平面,m、n是不重合的直线,给出下列命题:
是三个不重合的平面,m、n是不重合的直线,给出下列命题:
①若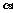 ⊥
⊥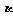 ,
,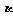 ⊥
⊥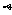 ,则
,则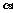 ⊥
⊥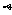 ;②若m∥
;②若m∥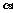 ,n∥
,n∥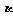 ,
, 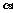 ⊥
⊥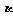 ,则m⊥n;③若
,则m⊥n;③若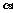 ∥
∥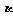 ,
,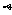 ∥
∥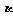 ,
,
则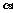 ∥
∥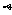 ④若m、n在
④若m、n在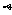 内的射影互相垂直,则m⊥n,其中错误命题有
个.
内的射影互相垂直,则m⊥n,其中错误命题有
个.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com