5．(2011·浙江五校联考)已知函数f(x)＝则f(2010)等于(　)

A．2008　 　　　　　　　　　　　　 B．2009

C．2010　 　　　　　　　　　　　　 D．2011

解析：当x>0时，f(x)－f(x－1)＝1，f(2010)＝f(2010)－f(2009)+f(2009)－f(2008)+…+f(1)－f(0)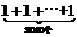+f(0)

＝+f(0)

＝2010+log₂1＝2010.

答案：C

4．设M＝{x|－2≤x≤2}，N＝{y|0≤y≤2}，函数f(x)的定义域为M，值域为N，则f(x)的图象可以是图中的(　)

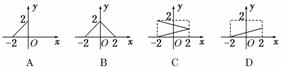
解析：由题图可知，A选项定义域为[－2,0]，C不是函数，D选项值域不是[0,2]，故排除A、C、D.

答案：B

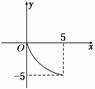
3．(2011·北海模拟)若函数y＝f(x)的图象是如图所示的一个四分之一的圆弧，则函数y＝f^－1(x)是(　)

A．y＝(－5≤x≤0)

B．y＝(0≤x≤5)

C．y＝5－(－5≤x≤0)

D．y＝5－(0≤x≤5)

解析：∵f(x)过(5，－5)，∴f^－1(x)过(－5,5)，排除A、B，又f(x)的值域是[－5,0]，∴f^－1(x)的定义域是[－5，0]，排除D.

答案：C

2．(2010·湖北高考)已知函数f(x)＝则f(f())＝(　)

A．4　 　　　　　　　　　　　　 B.

C．－4　 　　　　　　　　　　 D．－

解析：依题意得f()＝log₃＝－2，f(f())＝f(－2)＝2^－2＝.

答案：B

1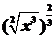．下列函数中，与函数y＝x相同的函数是(　)

A．y＝　　　　　 B．y＝

C．y＝lg10^x　 　　　　　　　　　　　　　 D．y＝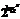

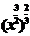解析：y＝＝x(x≠0)；

y＝　　 ＝x(x≥0)；

y＝lg10^x＝x(x∈R)；y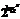＝＝x(x>0)．

答案：C

12．定义在正整数集上的函数f(x)对任意m，n∈N^*，都有f(m+n)＝f(m)+f(n)+4(m+n)－2，且f(1)＝1.

(1)求函数f(x)的表达式；

(2)若m²－tm－1≤f(x)对于任意的m∈[－1,1]，x∈N^*恒成立，求实数t的取值范围．

解：(1)取m＝1，则有f(n+1)－f(n)＝f(1)+4(1+n)－2＝4n+3，

当n≥2时，f(n)＝f(1)+[f(2)－f(1)]+[f(3)－f(2)]+…+[f(n)－f(n－1)]＝2n²+n－2，

又f(1)＝1，∴f(x)＝2x²+x－2(x∈N^*)．

(2)f(x)＝2(x+)²－，

∴x＝1时f(x)_min＝1，

由条件得m²－tm－1≤1在m∈[－1,1]上恒成立，

即m²－tm－2≤0，

若m＝0，则t∈R，

若0<m≤1，则t≥m－，即t≥－1，

若－1≤m<0，则t≤m－， 即t≤1，

综上－1≤t≤1.

11．设O为坐标原点，给定一个定点A(4,3)，而点B(x,0)在x轴的正半轴上移动，l(x)表示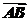的长，求函数y＝的值域．

解：依题意有x＞0，

l(x)＝＝，

所以y＝＝＝，

由于1－+＝25(－)²+，

所以 ≥，故0＜y≤，

即函数y＝的值域是(0，]．

10．求下列函数的定义域．

(1)y＝；

(2)y＝+；

(3)y＝.

解：(1)要使函数有意义，必须3x－2>0，

即x>.故所求函数的定义域为{x|x>}．

(2)要使函数有意义，必须

⇒

即x≥－1且x≠2.

故所求函数的定义域为{x|－1≤x<2或x>2}．

(3)要使函数有意义，必须满足

即1<x<3且x≠2.

故所求函数的定义域为{x|1<x<2或2<x<3}．

9．函数y＝|x+2|+的值域为________．

解析：y＝|x+2|+＝|x+2|+|x－3|

＝

当x≤－2时，－2x+1≥－2×(－2)+1＝5；

当x≥3时，2x－1≥2×3－1＝5，∴y≥5.

答案：[5，+∞)

8．若函数f(x)＝的定义域为R，则实数m的取值范围是________．

解析：若m＝0，则f(x)＝的定义域为R；

若m≠0，则Δ＝16m²－12m<0，得0<m<，

综上可知，所求的实数m的取值范围为[0，)．

答案：[0，)