
题目列表(包括答案和解析)
5.设x>0,y>0且x≠y,求证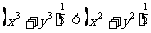
证明:由x>0,y>0且x≠y,要证明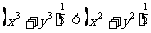
只需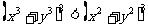 即
即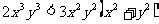
只需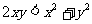
由条件,显然成立.∴原不等式成立
考点3 基本不等式在实际中的应用
题型1.处理恒成立的有关问题
例1. (2008·中山)若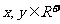 ,且
,且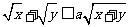 恒成立,则
恒成立,则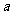 的最小值是________
的最小值是________
[解题思路]分离系数得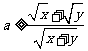 令
令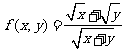 求最大值即可
求最大值即可
解析: 事实上求函数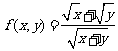 的最大值,即
的最大值,即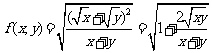 的最大值,运用基本不等式不难得到
的最大值,运用基本不等式不难得到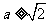 .
.
[名师指引]分离系数法是处理参数取值范围的常用方法.
题型2.处理函数应用题
.例2.(2008·梅县)某厂生产某种产品的年固定成本为250万元,每生产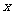 千件,需另投入成本为
千件,需另投入成本为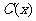 .当年产量不足80千件时,
.当年产量不足80千件时,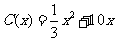 (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时,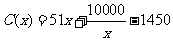 (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润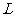 (万元)关于年产量
(万元)关于年产量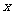 (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
[解题思路]凑出基本不等式的形式.
解析: (1)当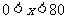 时,
时,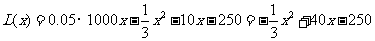
当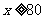 时,
时,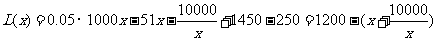
∴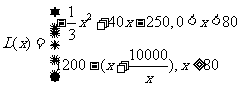
(2)当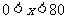 时,
时,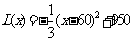 ,此时,当
,此时,当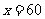 时,
时,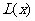 取得最大值
取得最大值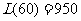 (万元);
(万元);
当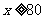 时,
时,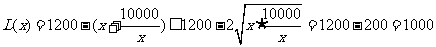
此时,当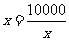 时,即
时,即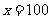 时,
时,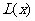 取得最大值1000万元.
取得最大值1000万元.
所以,当产量为100千件时,该厂在这一商品中所获利润最大,最大利润为1000万元.
[名师指引]形如函数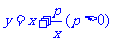 的形式求最值时可考虑用基本不等式,但要注意条件的限制,可借助函数的图像解题,必要时借助于导数.
的形式求最值时可考虑用基本不等式,但要注意条件的限制,可借助函数的图像解题,必要时借助于导数.
题型3.处理数列应用题
例3. 某乡为提高当地群众的生活水平,由政府投资兴建了甲、乙两个企业,2007年该乡从甲企业获得利润320万元,从乙企业获得利润720万元.以后每年上交的利润是:甲企业以1.5倍的速度递增,而乙企业则为上一年利润的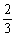 .根据测算,该乡从两个企业获得的利润达到2000万元可以解决温饱问题,达到8100万元可以达到小康水平.
.根据测算,该乡从两个企业获得的利润达到2000万元可以解决温饱问题,达到8100万元可以达到小康水平.
(1)若以2007年为第一年,则该乡从上述两个企业获得利润最少的一年是那一年,该年还需要筹集多少万元才能解决温饱问题?
(2)试估算2015年底该乡能否达到小康水平?为什么?
[解题思路]经审题抽象出数列模型
[解析](Ⅰ)若以2007年为第一年,则第n年该乡从这两家企业获得的利润为
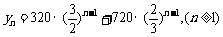 =
=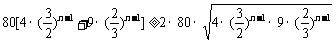 =
=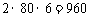
当且仅当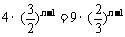 ,即n=2时,等号成立,
,即n=2时,等号成立,
所以第二年(2008年)上交利润最少,利润为960万元.
由2000–960=1040(万元)知:还需另筹资金1040万元可解决温饱问题.
(Ⅱ)2015年为第9年,该年可从两个企业获得利润
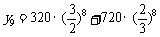
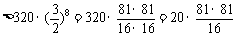
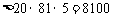
所以该乡到2015年底可以达到小康水平.
[名师指引]本题重点考查数列的相关知识,基本不等式起到了工具性的作用.
[新题导练]
4.已知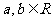 ,求证:
,求证: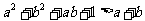
解析:∵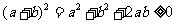 ∴
∴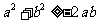 ① 又∵
① 又∵ ②
②  ③
③
由①②③得 ∴
∴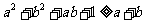 ,又不等式①、②、③中等号成立的条件分别为
,又不等式①、②、③中等号成立的条件分别为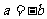 ,
,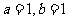 ,故不能同时成立,从而
,故不能同时成立,从而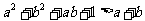 .
.
3. 已知一动直线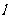 与两坐标轴的正半轴围成的三角形的面积的数值比直线
与两坐标轴的正半轴围成的三角形的面积的数值比直线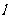 的纵、横截距之和大1,求这三角形面积的最小值.
的纵、横截距之和大1,求这三角形面积的最小值.
解析: 设直线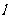 的方程
的方程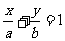 (a>0,b>0),则
(a>0,b>0),则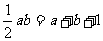 ,∵a+b>2
,∵a+b>2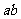 ,
,
∴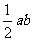 ≥
≥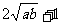 ,即
,即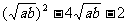 ≥0,解得
≥0,解得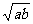 ≥
≥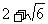 ,
,
∴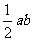 ≥
≥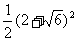 ,当a=b=2+
,当a=b=2+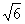 时,三角形面积的最小值为5+2
时,三角形面积的最小值为5+2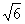
考点2 利用基本不等式证明
题型:用综合法证明简单的不等式
例1.
已知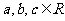 ,求证:
,求证: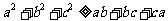 .
.
[解题思路]因为是轮换对称不等式,可考虑由局部证整体.
[解析] 
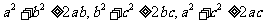 ,
,
相加整理得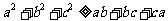 .
.
当且仅当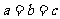 时等号成立.
时等号成立.
[名师指引]综合法证明不等式常用两个正数的算术平均数不小于它们的几何平均数这一结论,运用时要结合题目条件,有时要适当变形.
例2. 已知a,b为正数,求证: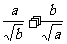 ≥
≥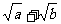 .
.
[解题思路]观察结构用基本不等式加以证明.
解析1:∵ a>0,b>0,
∴ 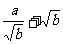 ≥
≥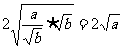 ,
,
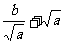 ≥
≥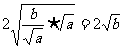 ,
,
两式相加,得
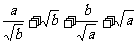 ≥
≥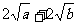 ,
,
∴ 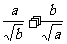 ≥
≥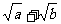 .
.
解析2. 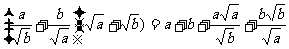 ≥
≥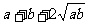
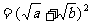 .
.
∴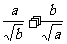 ≥
≥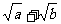 .
.
解析3.∵
a>0,b>0,∴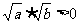 ,
,
∴ 欲证 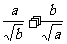 ≥
≥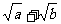 ,
,
即证 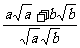 ≥
≥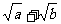 ,
,
只要证 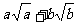 ≥
≥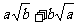 ,
,
只要证 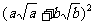 ≥
≥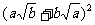 ,
,
即证  ≥
≥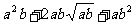 ,
,
只要证 a3+b3≥ab(a+b),
只要证 a2+b2-ab≥ab,
即证 (a-b)2≥0.
∵ (a-b)2≥0成立,∴ 原不等式成立 .
[名师指引]当要证明的不等式形式上比较复杂时,常通过分析法寻求证题思路.
“分析法”与“综合法”是数学推理中常用的思维方法,特别是这两种方法的综合运用能力,对解决实际问题有重要的作用. 这两种数学方法是高考考查的重要数学思维方法.
[新题导练]
2. .(2008·华附)已知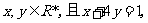 则
则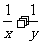 的最小值为
的最小值为
解析:∵ ,当且仅当
,当且仅当 时取等号.
时取等号.
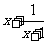
1.若 ,则
,则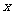 =_____时,
=_____时,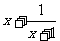 有最小值,最小值为_____.
有最小值,最小值为_____.
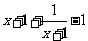
解析:∵ , ∴
, ∴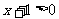 , ∴
, ∴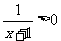 ,∴
,∴ =
=
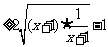
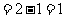 ,当且仅当
,当且仅当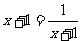 即
即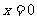 时
时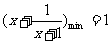 .
.
3.重难点:正确运用基本不等式证明不等式,会用基本不等式求某些函数的最值
(1) 灵活运用基本不等式处理不等关系
问题1. 已知正数x、y满足x+2y=1,求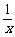 +
+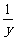 的最小值.
的最小值.
点拨:∵x、y为正数,且x+2y=1,
∴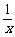 +
+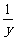 =(x+2y)(
=(x+2y)(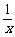 +
+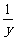 )
)
=3+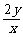 +
+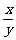 ≥3+2
≥3+2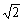 ,
,
当且仅当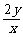 =
=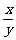 ,即当x=
,即当x=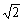 -1,y=1-
-1,y=1-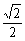 时等号成立.
时等号成立.
∴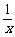 +
+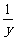 的最小值为3+2
的最小值为3+2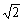 .
.
(2)注意取等号的条件
问题2. 已知两正数x,y 满足x+y=1,则z=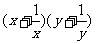 的最小值为
。
的最小值为
。
点拨:
错解1、因为对a>0,恒有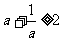 ,从而z=
,从而z=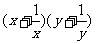
 4,所以z的最小值是4。
4,所以z的最小值是4。
错解2、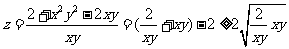
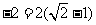 ,所以z的最小值是
,所以z的最小值是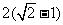 。
。
错因分析:解一等号成立的条件是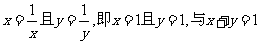 相矛盾。解二等号成立的条件是
相矛盾。解二等号成立的条件是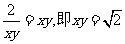 ,与
,与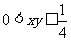 相矛盾。
相矛盾。
解析:z=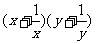 =
=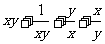 =
=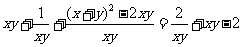 ,令t=xy, 则
,令t=xy, 则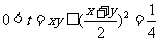 ,由
,由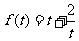 在
在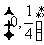 上单调递减,故当t=
上单调递减,故当t=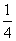 时
时 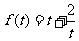 有最小值
有最小值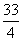 ,所以当
,所以当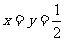 时z有最小值
时z有最小值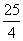 。
。
★ 热 点 考 点 题 型 探 析★
考点1 利用基本不等式求最值(或取值范围)
题型1. 当积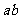 为定值时,求和
为定值时,求和 最小值
最小值
例1 . 已知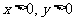 且满足
且满足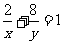 ,求
,求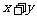 的最小值.
的最小值.
[解题思路]利用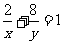 ,构造均值不等式
,构造均值不等式
解析:∵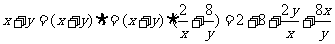 ,
,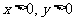 ,∴
,∴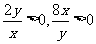
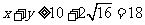 ,当且仅当
,当且仅当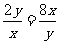 时等号成立,即
时等号成立,即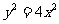 ,∴
,∴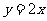 ,又
,又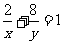 , ∴
, ∴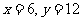 ∴当
∴当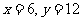 时,
时,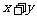 有最小值18.
有最小值18.
[名师指引]利用基本不等式求最值要注意“一正二定三相等”即(1)要求各数均为正数;(2)要求“和”或“积”为定值;(3)要注意是否具备等号成立的条件.
题型2. 当和 为定值时, 求积
为定值时, 求积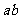 最大值
最大值
例2. 已知x>0,y>0,且3x+4y=12,求lgx+lgy的最大值及此时x、y的值.
[解题思路]这是条件最值问题,但目标式与已知条件的联系较隐蔽,不易发现. 应将lgx+lgy转化成lgxy考虑.
解析∵x>0,y>0,3x+4y=12,
∴ 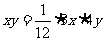 ≤
≤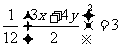 ,
,
∴lgx+lgy=lgxy≤lg3 .
由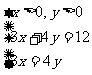 解得
解得 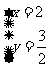
∴当x=2,y=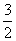 时,lgx+lgy取得最大值lg3 .
时,lgx+lgy取得最大值lg3 .
[名师指引]利用基本不等式求最值是高考中最常考的方法之一.
题型3.灵活运用基本不等式求取值范围
例3. 若正数a,b满足ab=a+b+3,则ab的取值范围是_______ .
[解题思路]可通过多种途经将等式化为可利用重要不等式的不等关系求解.
解法一 由a、b∈R+,由重要不等式得a+b≥2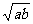 ,
,
则ab=a+b+3≥2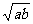 +3,
+3,
即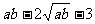 ≥
≥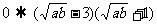 ≥
≥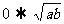 ≥3,
≥3,
∴ ab≥9 .
解法二 a、b为正数,∴ ab=a+b+3≥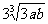 >0,
>0,
两边立方得 a3b3≥34ab a2b2≥34,∵ab>0,∴ab≥9 .
a2b2≥34,∵ab>0,∴ab≥9 .
解法三 原条件式变为ab-3=a+b, ①
∵ a、b均为正数,故①式两边都为正数,两边平方得
a2b2-6ab+9=a2+b2+2ab,
∵ a2+b2≥2ab,∴ a2b2-6ab+9≥4ab,
即a2b2-10ab+9≥0,(ab-1)(ab-9)≥0,
由①式可知ab>3,∴ ab≥9 .
解法四 把a、b∈R+看作一元二次方程的两个根,此方程为
x2+(3-ab)x+ab=0,则△=(3-ab)2-4ab≥0,
即 (ab)2-10ab+9≥0,∴ (ab-9)(ab-1)≥0,
∵ab-1=a+b+2>0成立,∴ ab≥9 .
解法五 由已知得a(b-1)=b+3,显然a>1,∴ 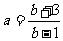 ,
,
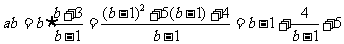 ≥
≥ ,
,
即ab≥9 .
[名师指引]本题用了转化思想(等式转化为不等式)、方程思想、函数思想,这是解决数学问题经常用的思想方法.
[新题导练]
2.难点:利用基本不等式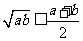 求最大值、最小值
求最大值、最小值
1.重点:理解基本不等式 等号成立条件,掌握用基本不等式证明不等式
等号成立条件,掌握用基本不等式证明不等式
会用基本不等式解决简单的最大(小)值问题.
3.拓展:若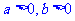 时,
时,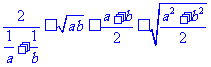 ,当且仅当
,当且仅当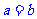 时等号成立.
时等号成立.
★ 重 难 点 突 破 ★
1.基本形式: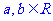 ,则
,则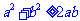 ;
;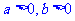 ,则
,则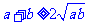 ,当且仅当
,当且仅当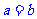 时等号成立.
时等号成立.
2求最值:当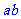 为定值时,
为定值时,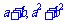 有最小值;当
有最小值;当 或
或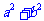 为定值时,
为定值时,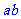 有最大值(
有最大值(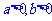 ).
).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com