
题目列表(包括答案和解析)
6.讨论函数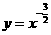 的定义域、值域及函数值y随x变化规律,并画出其图象.
的定义域、值域及函数值y随x变化规律,并画出其图象.
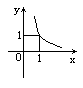 [解析]
[解析] 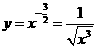 ,函数的定义域
,函数的定义域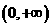 ,值域
,值域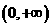 .由图象可知,在区间(0,+∞)上函数值y随x的增加而减小.
.由图象可知,在区间(0,+∞)上函数值y随x的增加而减小.
5.函数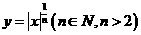 的图象只可能是( )
的图象只可能是( )
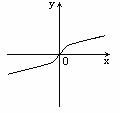
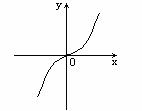
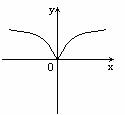
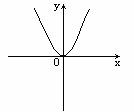 A
B
C
D
A
B
C
D
[解析]显然,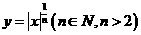 是偶函数,故可排除A和B,又
是偶函数,故可排除A和B,又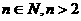 ,所以应选择C
,所以应选择C
综合提高训练:
4.(2007·广东实验中学)设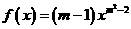 ,如果
,如果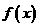 是正比例函数,则m=______,如果
是正比例函数,则m=______,如果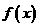 是反比例函数,则m=______,如果
是反比例函数,则m=______,如果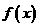 是幂函数,则m=______
是幂函数,则m=______
[解析] 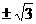 ,
, ,2;若
,2;若 是正比例函数,则
是正比例函数,则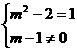 ,即
,即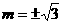 ;若
;若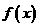 是反比例函数,则
是反比例函数,则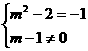 ,即
,即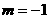 ;若
;若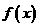 是幂函数,则
是幂函数,则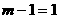 ,即
,即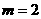
3.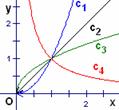 如图所示,曲线是幂函数
如图所示,曲线是幂函数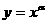 在第一象限内的图像,已知
在第一象限内的图像,已知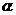 分别取
分别取 四个值,则相应图像依次为:
四个值,则相应图像依次为:
[解析] 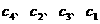 ;根据幂函数的图象特征知,当
;根据幂函数的图象特征知,当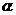 分别取
分别取 时,相应图像依次为
时,相应图像依次为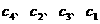
2.(2007·山东改编)设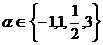 ,则使函数
,则使函数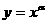 的定义域为R且为奇函数的所有
的定义域为R且为奇函数的所有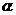 的值为
的值为
[解析] 1,3;当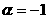 及
及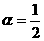 时,
时,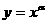 的定义域都不是R,当
的定义域都不是R,当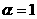 及
及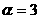 时,
时,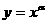 的定义域都都是R,并且都是奇函数
的定义域都都是R,并且都是奇函数
1.在函数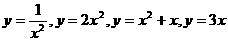 中,幂函数的个数为( )
中,幂函数的个数为( )
A.0 B.1 C.2 D.3
[解析] B;显然,根据幂函数可知,只有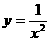 是幂函数
是幂函数
3.求函数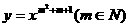 的定义域、值域,并判断其单调性
的定义域、值域,并判断其单调性
[解析]因为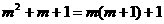 必为奇数,并且
必为奇数,并且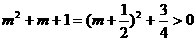
所以函数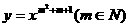 的定义域为
的定义域为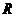 ,类比
,类比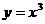 的图象可知,所求函数的值域为
的图象可知,所求函数的值域为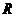 ,并且在
,并且在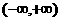 上为增函数
上为增函数
[备选例题]已知函数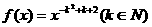 满足
满足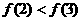
(1)求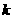 的值并求出相应的
的值并求出相应的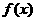 的解析式;
的解析式;
(2)对于(1)中得到的函数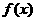 ,试判断是否存在
,试判断是否存在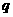 ,使函数
,使函数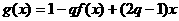 在区间
在区间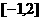 上的值域为
上的值域为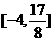 ?若存在,求出
?若存在,求出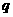 ;若不存在,说明理由
;若不存在,说明理由
[解题思路]利用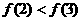 求
求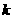 ,易得
,易得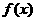 的解析式,再利用
的解析式,再利用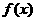 表达
表达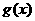 从而求解
从而求解
[解析](1)因为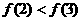 ,所以
,所以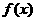 在第一象限是增函数
在第一象限是增函数
故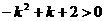 ,解得
,解得
又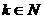 ,所以
,所以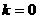 或
或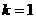 ,当
,当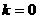 或
或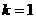 时,
时,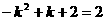
所以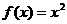
(2)假设存在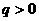 满足题设,由(1)知,
满足题设,由(1)知,
因为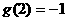 ,所以两个最值点只能在端点
,所以两个最值点只能在端点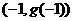 和顶点
和顶点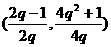 处取到
处取到
而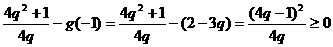 ,所以
,所以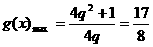
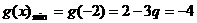 ,解得
,解得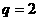 ,所以存在
,所以存在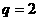 满足题意
满足题意
★抢分频道
基础巩固训练:
2.若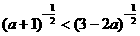 ,则
,则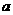 的取值范围是
的取值范围是
[解析] 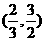 ;令
;令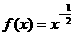 ,则
,则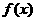 在
在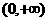 上是减函数,故得
上是减函数,故得
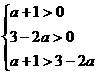 ,解得
,解得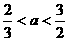
|
|
 |
 |
 |
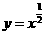 |
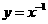 |
|
定义域 |
R |
R |
R |
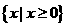 |
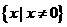 |
|
奇偶性 |
奇 |
奇 |
奇 |
非奇非偶 |
奇 |
|
在第Ⅰ象限的增减性 |
在第Ⅰ象限单调递增 |
在第Ⅰ象限单调递增 |
在第Ⅰ象限单调递增 |
在第Ⅰ象限单调递增 |
在第Ⅰ象限单调递减 |
幂函数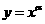 (
( R,
R,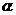 是常数)的图像在第一象限的分布规律是:
是常数)的图像在第一象限的分布规律是:
 ①所有幂函数
①所有幂函数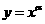 (
( R,
R,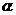 是常数)的图像都过点
是常数)的图像都过点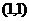 ;
;
②当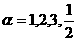 时函数
时函数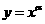 的图像都过原点
的图像都过原点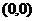 ;
;
③当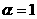 时,
时,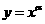 的的图像在第一象限是第一象限的平分线(如
的的图像在第一象限是第一象限的平分线(如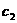 );
);
④当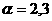 时,
时,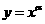 的的图像在第一象限是“凹型”曲线(如
的的图像在第一象限是“凹型”曲线(如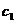 )
)
⑤当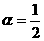 时,
时,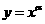 的的图像在第一象限是“凸型”曲线(如
的的图像在第一象限是“凸型”曲线(如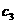 )
)
⑥当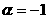 时,
时,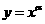 的的图像不过原点
的的图像不过原点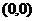 ,且在第一象限是“下滑”曲线(如
,且在第一象限是“下滑”曲线(如 )
)
★重、难点突破
重点:幂函数的概念、几个特殊幂函数的图像与性质。
难点:综合运用几个特殊幂函数的图像与性质解决问题。
重难点:幂函数性质的拓展
当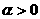 时,幂函数
时,幂函数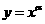 有下列性质:
有下列性质:
(1)图象都通过点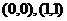 ;
;
(2)在第一象限内都是增函数;
(3)在第一象限内,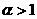 时,图象是向下凸的;
时,图象是向下凸的;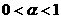 时,图象是向上凸的;
时,图象是向上凸的;
(4)在第一象限内,过点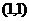 后,图象向右上方无限伸展。
后,图象向右上方无限伸展。
当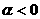 时,幂函数
时,幂函数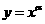 有下列性质:
有下列性质:
(1)图象都通过点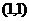 ;
;
(2)在第一象限内都是减函数,图象是向下凸的;
(3)在第一象限内,图象向上与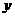 轴无限地接近;向右无限地与
轴无限地接近;向右无限地与 轴无限地接近;
轴无限地接近;
(4)在第一象限内,过点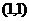 后,
后,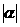 越大,图象下落的速度越快。
越大,图象下落的速度越快。
无论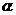 取任何实数,幂函数
取任何实数,幂函数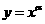 的图象必然经过第一象限,并且一定不经过第四象限。
的图象必然经过第一象限,并且一定不经过第四象限。
★热点考点题型探析
考点 幂函数的概念、图象和性质
题型1:利用幂函数的单调性比较大小
[例1](中山市09届月考)已知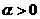 ,试比较
,试比较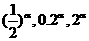 的大小;
的大小;
[解题思路]欲比较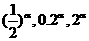 这几个数的大小,因为它们的指数相同,应考虑某个幂函数的单调性
这几个数的大小,因为它们的指数相同,应考虑某个幂函数的单调性
[解析] 在
在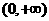 上单调递增,又
上单调递增,又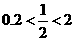 ∴
∴ 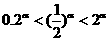 .
.
[名师指引]比较几个数式的大小,是解题过程中常常遇到的知识考点,往往都要用到函数的单调性,我们应该熟练掌握规定的几个特殊幂函数的单调性、奇偶性及图像特征.
题型2:由幂函数的性质确定解析式
[例2] 已知函数f(x)=x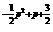 (p∈Z)在(0,+∞)上是增函数,且在其定义域上是偶函数。
(p∈Z)在(0,+∞)上是增函数,且在其定义域上是偶函数。
(1)求p的值,并写出相应的函数f(x)的解析式。
(2)对于(1)中求得的函数f(x),设函数g(x)=-qf[f(x)]+(2q-1)f(x)+1,问是否存在实数q(q<0),使得g(x)在区间(-∞,-4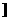 上是减函数,且在区间(-4,0)上是增函数。若存在,请求出来;若不存在,请说明理由。
上是减函数,且在区间(-4,0)上是增函数。若存在,请求出来;若不存在,请说明理由。
[解题思路](1)由函数f(x)=x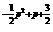 (p∈Z)在(0,+∞)上是增函数即可知
(p∈Z)在(0,+∞)上是增函数即可知
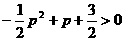 ,又由p∈Z即可确定p的值
,又由p∈Z即可确定p的值
(2)根据(1)的结果,利用函数单调性的定义进行探索求解。
[解析] (1)若y=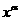 在x∈(0,+∞)上是递增函数,则有α>0。
在x∈(0,+∞)上是递增函数,则有α>0。
∵f(x)在(0,+∞)上是增函数,
∴-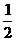 p2+p+
p2+p+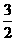 >0 解得:-1<p<3,而p∈Z ∴p=0,1,2
>0 解得:-1<p<3,而p∈Z ∴p=0,1,2
当p=0或2时,有f(x)=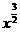 不是偶函数,故p=1,此时,f(x)=x2。
不是偶函数,故p=1,此时,f(x)=x2。
 (2)设t=x2,由g(x)在(-∞,-4
(2)设t=x2,由g(x)在(-∞,-4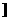 上是减函数,在(-4,0)上是增函数,而t=x2在[16,+∞
上是减函数,在(-4,0)上是增函数,而t=x2在[16,+∞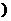 和(0,16)上都是增函数,得h(t)=-qt2+(2q-1)t+1在(0,16)上是增函数,在[16,+∞
和(0,16)上都是增函数,得h(t)=-qt2+(2q-1)t+1在(0,16)上是增函数,在[16,+∞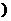 上是减函数,从而可得
上是减函数,从而可得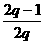 =16,∴q=-
=16,∴q=-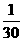
故存在实数q=-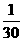 ,使得g(x)在(-∞,-4
,使得g(x)在(-∞,-4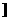 上是减函数,且在(-4,0)上是增函数。
上是减函数,且在(-4,0)上是增函数。
[名师指引](1)解决这类问题要紧扣幂函数的定义和性质,依单调性从其指数入手;(2)复合函数的单调规则是我们处理复合函数的单调性的重要依据。
[新题导练]
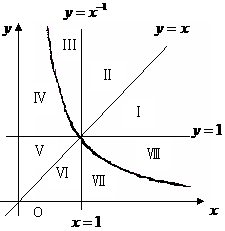
1.(珠海斗门中学09届月考)幂函数①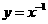 ,
,
②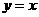 及直线③
及直线③ ,④
,④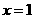 将直角坐标系第一象限分成八个“卦限”:
将直角坐标系第一象限分成八个“卦限”:
Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ,Ⅵ,Ⅶ,Ⅷ(如图所示),
那么幂函数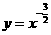 的图象在第一象限中经过的“卦限”是( )
的图象在第一象限中经过的“卦限”是( )
A.Ⅳ,Ⅶ ;B. Ⅳ,Ⅷ;C.Ⅲ,Ⅷ;D. Ⅲ,Ⅶ
[解析] D;由于当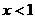 时,
时,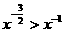 ,当
,当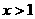 时,
时,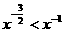 ,故幂函数
,故幂函数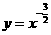 的图象在第一象限中经过的“卦限”是Ⅲ,Ⅶ
的图象在第一象限中经过的“卦限”是Ⅲ,Ⅶ
一般地,形如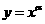 (
( R)的函数称为幂函数,其中
R)的函数称为幂函数,其中 是自变量,
是自变量,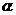 是常数
是常数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com