9．已知函数f(x)＝ax－x²的最大值不大于，当x∈[，]时，f(x)≥，则a的值为________．

解析：f(x)＝－(x－)²+a²，

由f(x)_max＝a²≤得－1≤a≤1，

函数f(x)的图象的对称轴为x＝，

当－1≤a<时，－≤<，[，]是f(x)的递减区间，而f(x)≥，

即f(x)_min＝f()＝－≥，得a≥1，与－1≤a<矛盾，即不存在这样的a值；

当≤a≤1时，≤≤，结合图象知道区间[，]的端点离对称轴的距离大，故f(x)_min＝f()＝－≥，a≥1，而≤a≤1，得a＝1，

∴a＝1.

综上可知，a＝1.

答案：1

8．定义在[－1,1]的偶函数f(x)，当x∈[0,1]时为减函数，则不等式：f(－x)<f(x)的解集为________．

解析：因为函数f(x)是定义在[－1,1]的偶函数，且当x∈[0,1]时为减函数，所以不等式f(－x)<f(x)应满足

即

解得－≤x<.

答案：[－，)

7．(文)函数y＝在(－2，+∞)上为增函数，则a的取值范围是________．

解析：y＝＝1－，

依题意，得函数的单调增区间为(－∞，－a)、(－a，+∞)，

要使y在(－2，+∞)上为增函数，只要－2≥－a，即a≥2.

答案：a≥2

(理)若f(x)＝－x²+2ax与g(x)＝在区间[1,2]上都是减函数，则a的取值范围是________．

解析：f(x)＝－(x－a)²+a²，当a≤1时，f(x)在[1,2]上是减函数，g(x)＝，当a>0时，g(x)在[1,2]上是减函数，则a的取值范围是(0,1]．

答案：(0,1]

6．(文)函数f(x)＝(m－1)x²+2mx+3为偶函数，则f(x)在区间(－5，－3)上(　)

A．先减后增　 　　　　　　　　　　　　 B．先增后减

C．单调递减　 　　　　　　　　　　　　 D．单调递增

解析：当m＝1时，f(x)＝2x+3不是偶函数，当m≠1时，f(x)为一元二次函数，要使其为偶函数，则其对称轴应为y轴，故需m＝0，此时f(x)＝－x²+3，其图象的开口向下，所以函数f(x)在(－5，－3)上单调递增．

答案：D

(理)已知定义在(0，+∞)上的函数f(x)为单调函数，且f(x)·f(f(x)+)＝1，则f(1)＝(　)

A．1　 　　　　　　　　　　　　　　　 B.或

C.　 　　　　　　　　　　　　 D.

解析：设f(1)＝b，则令x＝1，

则由题意知f(1)·f(f(1)+)＝1，

即f(b+1)＝，令x＝b+1，

则有f(b+1)·f(f(b+1)+)＝1，

即·f(+)＝1，即f(+)＝b＝f(1)，

又因为函数f(x)在(0，+∞)上是单调函数，

所以+＝1，

即b²－b－1＝0，

解得b＝.

答案：B

5．(2011·重庆模拟)已知定义域为R的奇函数f(x)满足：(x₁－x₂)[f(x₁)－f(x₂)]＞0，其中x₁≠x₂，那么使不等式f(x)+f(x²)＜0成立的实数x的取值范围为(　)

A．(－1,0)　 　　　　　　　　　　　 B．(－∞，－1)

C．(0,1)　 　　　　　 　　　　　　　 D．(－1,1)

解析：定义域为R的奇函数f(x)满足：(x₁－x₂)·[f(x₁)－f(x₂)]＞0，其中x₁≠x₂，即函数为增函数，不等式f(x)+f(x²)＜0即f(x²)＜－f(x)＝f(－x)，所以，x²＜－x，解得－1＜x＜0.

答案：A

4．已知函数f(x)＝x²－2ax+a在区间(－∞，1)上有最小值，则函数g(x)＝在区间(1，+∞)上一定(　)

A．有最小值　 　　　　　　　　　　　　 B．有最大值

C．是减函数　 　　　　　　　　　　　　 D．是增函数

解析：由题意a<1，

故函数g(x)＝x+－2a在[，+∞)上为增函数．

答案：D

3．函数y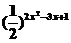＝的递减区间为(　)

A．(1，+∞) 　　　　　　　　　　　　 B．(－∞，]

C．(，+∞)　 　　　　　　　　　　　　 D．[，+∞)

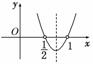解析：作出t＝2x²－3x+1的示意图如图所示，

∵0<<1，

∴y＝()^t单调递减．

要使y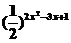＝递减，

只需x∈[，+∞)．

答案：D

2．(2011·西宁模拟)已知函数f(x)＝ 在R上单调递减，则实数a的取值范围是(　)

A．(－∞，)　 　　　　　　　　　　　　 B．(，+∞)

C．[，)　 　　　　　　　　　　　　　　　 D．R

解析：由题意可得：

∴≤a<.

答案：C

1．已知偶函数f(x)在区间[0，+∞)上单调增加，则满足f(2x－1)<f()的x的取值范围是(　)

A．(，)　　　　　 B．[，)

C．(，)　 　　　　　　　　　　　　　　　 D．[，)

解析：当2x－1≥0，即x≥时，

由于函数f(x)在区间[0，+∞)上单调增加，

则由f(2x－1)<f()得2x－1<，

即x<，故≤x<；

当2x－1<0，即x<时，

由于函数f(x)是偶函数，

故f(2x－1)＝f(1－2x)，此时1－2x>0，

由f(2x－1)<f()得1－2x<，

即x>，故<x<.

综上可知x的取值范围是(，)．

答案：A

9．(2010·重庆高考)已知函数f(x)满足：f(1)＝，4f(x)f(y)＝f(x+y)+f(x－y)(x，y∈R)，则f(2 010)＝________.

解析：依题意得4f(1)f(0)＝f(1)+f(1)，

f(0)＝2f(1)＝；

f(n+1)+f(n－1)＝4f(n)f(1)＝f(n)，

所以f(n+1)＝f(n)－f(n－1)，

记a_n＝f(n)(其中n∈N^*)，则有a_n+1＝a_n－a_n－1(n≥2)，a_n+2＝a_n+1－a_n＝－a_n－1，

a_n+3＝a_n+2－a_n+1＝－a_n，

a_n+6＝－a_n+3＝a_n，

故数列{a_n}的项以6为周期重复出现．

注意到2 010＝6×335，因此有a_{2 010}＝a₆ ＝f(0)＝，

即f(2 010)＝.