6．正方体ABCD－A₁B₁C₁D₁的棱长为1，E、F分别为BB₁、CD的中点，则点F到平面A₁D₁E的距离为　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A. 　　　　　　 　B.　 　　　　　　　 C.　　　　　　 　 D.

答案：C

解析：取，，分别为x轴、y轴、z轴建立空间直角坐标系，并连结A₁F，如图所示，

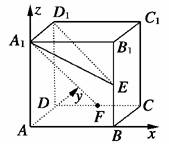
则A₁(0,0,1)，E(1,0，)，D(0,1,0)，F(，1,0)，D₁(0,1,1)．

∴＝(1,0，－)，

＝(0,1,0)，

设平面A₁D₁E的一个法向量为n＝(x，y，z)，则

，即，令z＝2，则x＝1.

∴平面A₁D₁E的一个法向量为n＝(1,0,2)．

又＝(，1，－1)，

∴点F到平面A₁D₁E的距离

d＝＝＝.

5．(2009·昆明质检)如图，已知正四棱柱ABCD－A₁B₁C₁D₁的底面边长等于2，侧棱长等于，M是B₁C₁的中点，则直线AB₁与直线CM所成角的余弦值为　　　　　　　　　　 (　)

A.　 　　　　　 B.　 　　　　　 C.　 　　　　　 D.

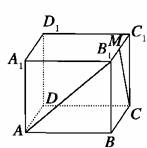
答案：A

解析：建立坐标系如图，则A(2,0,0)，B₁(2,2，)，C(0,2,0)，M(1,2，)，＝(0,2，)，＝(1,0，)，cos〈、〉＝，故选A.

4．已知A(2，－5,1)、B(2，－2,4)，C(1，－4,1)，则向量与的夹角为　　 (　)

A．30°　 　B．45° 　　C．60° 　　D．90°

答案：C

解析：由已知得＝(0,3,3)，＝(－1,1,0)．

所以cos?，?＝＝＝，

所以向量与的夹角为60°，故选C.

3．设点C(2a－1，a+1,2)在点P(2,0,0)、A(1，－3,2)、B(8，－1,4)确定的平面上，则a等于　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．16　 B．4　 C．2　 D．8

答案：A

解析：＝(－1，－3,2)，＝(6，－1,4)，根据共面向量定理，设＝x+y(x，y∈R)则

(2a－1，a+1,2)＝x(－1，－3,2)+y(6，－1,4)

＝(－x+6y，－3x－y,2x+4y)，

∴解得x＝－7，y＝4，a＝16.

2．已知点A(2,3－μ，－1+υ)关于x轴的对称点A′(λ，7，－6)，则λ、μ、υ的值为(　)

A．λ＝－2，μ＝－4，υ＝－5　　　 B．λ＝2，μ＝－4，υ＝－5

C．λ＝2，μ＝10，υ＝8　　　　　 D．λ＝2，μ＝10，υ＝7

答案：D

解析：两个点关于x轴对称，那么这两个点的横坐标不变，而纵坐标和竖坐标均相差一个符号，也就是这两个点的纵坐标与竖坐标均互为相反数，故有λ＝－2,7＝－(3－μ)，－6＝－(－1+υ)，所以λ＝2，μ＝10，υ＝7，应选D.

1．已知向量a＝(1,1,0)，b＝(－1,0,2)，且ka+b与2a－b互相垂直，则k的值是(　)

A．1　 　　　　　 B. 　　　　　　　 　C.　　　　　　　　　　 　 D.

答案：D

解析：ka+b＝k(1,1,0)+(－1,0,2)＝(k－1，k,2)，

2a－b＝2(1,1,0)－(－1,0,2)＝(3,2，－2)．

(k－1，k,2)·(3,2，－2)＝0，k＝，故选D.

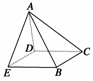
16．如图四棱锥A－BCDE中，AD⊥底面BCDE，AC⊥BC，AE⊥BE.

(1)求证：A、B、C、D、E五点共球；

(2)若∠CBE＝90°，CE＝，AD＝1，求B、D两点的球面距离．

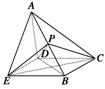解析：(1)证明：取AB的中点P，连结PE，PC，PD，由题设条件知△AEB、△ADB、△ABC都是直角三角形．

故PE＝PD＝PC＝AB＝PA＝PB.

所以A、B、C、D、E五点在同一球面上．

(2)解：由题意知四边形BCDE为矩形，

所以BD＝CE＝，

在Rt△ADB中，AB＝2，AD＝1，

∴∠DPB＝120°，D、B的球面距离为π.

15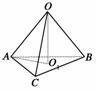．设A、B、C是半径为1的球面上的三点，B、C两点间的球面距离为，点A与B、C两点间的球面距离均为，O为球心，求：

(1)∠AOB、∠BOC的大小；

(2)球心O到截面ABC的距离．

解析：(1)如图，因为球O的半径为1，B、C两点间的球面距离为，点A与B、C两点间的球面距离均为，所以∠BOC＝，∠AOB＝∠AOC＝，

(2)因为BC＝1，AC＝AB＝，所以由余弦定理得cos∠BAC＝，sin∠BAC＝，设截面圆的圆心为O₁，连结AO₁，则截面圆的半径r＝AO₁，由正弦定理得r＝

＝，所以OO₁＝＝.

14．在球心同侧有相距9cm的两个平行截面，它们的面积分别为49πcm²和400πcm²，求球的表面积和体积．

解析：如图，两平行截面被球大圆所在平面截得的交线分别为AO₁、BO₂，则AO₁∥BO₂.

若O₁、O₂分别为两截面圆的圆心，则由等腰三角形性质易知OO₁⊥AO₁，OO₂⊥BO₂，

设球半径为R，∵πO₂B²＝49π，

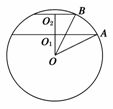∴O₂B＝7cm，同理O₁A＝20cm.

设OO₁＝xcm，则OO₂＝(x+9)cm.

在Rt△OO₁A中，R²＝x²+20²，

在Rt△OO₂B中，R²＝(x+9)²+7²，

∴x²+20²＝7²+(x+9)²，解得x＝15cm.

∴R＝25cm，∴S_球＝2500πcm²，

V_球＝πR³＝πcm³.

13．把地球当作半径为R的球，地球上A、B两地都在北纬45°，A、B两点的球面距离是R，A点在东经20°，求B点的位置．

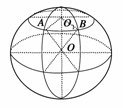解析：如图，求B点的位置即求B点的经度，设B点在东经α，

∵A、B两点的球面距离是R.

∴∠AOB＝，因此三角形AOB是等边三角形，∴AB＝R，

又∵∠AO₁B＝α－20°(经度差)

问题转化为在△AO₁B中借助AO₁＝BO₁＝AOcos45°＝R，

求出∠AO₁B＝90°，则α＝110°，同理：B点也可在西经70°，即B点在北纬45°东经110°或西经70°.