6、如图，在一块三角形区域ABC中，∠C=90°，边AC=8，BC=6，现要在△ABC内建造一个矩形水池DEFG，如图的设计方案是使DE在AB上。　

⑴求△ABC中AB边上的高h;

⑵设DG=x,当x取何值时，水池DEFG的面积最大？

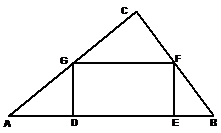⑶实际施工时，发现在AB上距B点1.85的M处有一棵大树，问：这棵大树是否位于最大矩形水池的边上？如果在，为保护大树，请设计出另外的方案，使三角形区域中欲建的最大矩形水池能避开大树。(本小题10分)

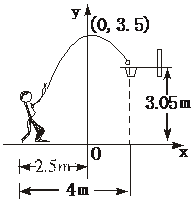
4、如图，一位运动员在距篮下4米处跳起投篮，球运行的路线是抛物线，当球运行的水平距离为2.5米时，达到最大高度3.5米，然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.

(1)建立如图所示的直角坐标系，求抛物线的表达式;

(2)该运动员身高1.8米，在这次跳投中，球在头顶上方0.25米处出手，问：球出手时，他跳离地面的高度是多少. (本小题8分)

4、如图14-1是某段河床横断面的示意图.查阅该河段的水文资料，得到下表中的数据：

(1)请你以上表中的各对数据(x，y)作为点的坐标，

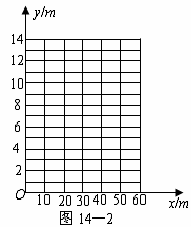尝试在图14-2所示的坐标系中画出y关于x的函数图象；

(2)①填写下表：

x	5	10	20	30	40	50

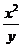　　 ②根据所填表中数据呈现的规律，猜想出用x表示y 的二次函数的表达式：　　 　　　　　　　　　　.

(3)当水面宽度为36米时，一艘吃水深度(船底部到水面的距离)为1.8米的货船能否在这个河段安全通过？为什么？(本小题8分)

2、某商场以每件20元的价格购进一种商品，试销中发现，这种商品每天的销售量m(件)与每件的销售价x(元)满足关系：m=140－2x.

(1)写出商场卖这种商品每天的销售利润y与每件的销售价x间的函数关系式;

(2)如果商场要想每天获得最大的销售利润，每件商品的售价定为多少最合适？最大销售利润为多少？(本小题8分)

1、已知抛物线y＝ax²+(b-1)x+2的图象经过点(1，4)，(-1，2)，求抛物线的解析式。(本小题7分)

7、函数y=ax²-a与y=a/x(a≠0)在同一直角坐标系中的图象可能是(　　 )

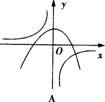
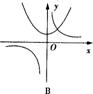
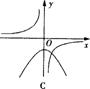
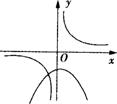
A　　　　　　　 B　　　　　　　 C　　　　　　　　 D

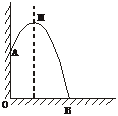　 8、某幢建筑物，从10 m高的窗口A，用水管向外喷水，喷出的水流呈抛物线状(抛物线所在的平面与墙面垂直，如图5，如果抛物线的最高

点M离墙1m，离地面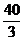m，则水流落地点B离墙的距离OB是(　 )

A.2 m 　　B.3 m　 　C.4 m　　　 D.5 m

6、如图，铅球运动员掷铅球的高度y(m)与水平距

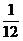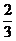离x(m)之间的函数关系式是 y =－x²+x+，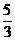

则该运动员此次掷铅球的成绩是(　　 )

A.6 m　　 　B.12 m　　 C.8 m　　　 D.10 m

5、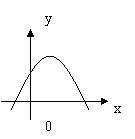二次函数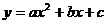的图象如右图所示，

　 则下列结论中正确的是：(　 )

　 A　 a>0　 b<0　 c>0　　 B　 a<0　 b<0　 c>0

　 C　 a<0　 b>0　 c<0　　 D　 a<0　 b>0　 c>0

4、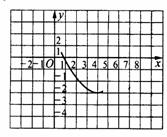对于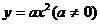的图象下列叙述正确的是(　　 )

A、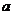的值越大，开口越大　 　B、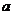的值越小，开口越小

C、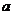的绝对值越小，开口越大 D、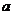的绝对值越小，开口越小

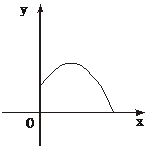
3、已知抛物线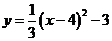的部分图象(如图所示)，图象再次与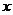轴相交时的

坐标是(　 ) A、(5,0)　　　 B、(6,0)　　 C、(7,0)　 　D、(8,0)