
题目列表(包括答案和解析)
23、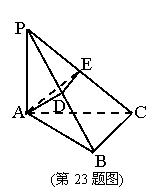 如图,DABC是直角三角形,ÐABC=900,AP^平面ABC,且AP=AB,点D是PB的中点,点E是PC上的一点,
如图,DABC是直角三角形,ÐABC=900,AP^平面ABC,且AP=AB,点D是PB的中点,点E是PC上的一点,
(1)当DE//BC时,求证:直线PB^平面ADE;
(2)当DE^PC时,求证:直线PC^平面ADE;
(3)当AB=BC时,求二面角A-PC-B的大小.
(1)证:∵AP=AB,点D是PB的中点,∴AD^PB,
∵AP^平面ABC,BCÌ平面ABC,
∴AP^BC,∵AB^BC,∴BC^平面PAB,
∵PBÌ平面PAB,∴BC^PB,
∵DE//BC,∴DE^PB,∴PB^平面ADE. (3¢)
(2)证:∵BC^平面PAB,ADÌ平面PAB,∴BC^AD,
又AD^PB,∴AD^平面PBC,∵PCÌ平面PBC,∴AD^PC,
又DE^PC,∴PC^平面ADE. (6¢)
(3)由(2)可知,当DE^PC时,PC^平面ADE,
∴ÐAED是二面角A-PC-B的平面角. (7¢)
设AP=a,则AB=BC=a,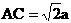 ,
,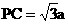 ,(8¢)
,(8¢)
∵AD^平面PBC,DEÌ平面PBC,∴AD^DE,
在RtDADE中,可求得,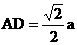 ,
,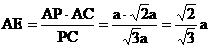 ,(9¢)
,(9¢)
∴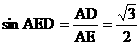 ,∴ÐAED=600,
,∴ÐAED=600,
∴二面角A-PC-B的大小为600. (10¢)
17、 2 ;18、(x+1)2+(y-2)2=4;19、 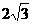 ;20、 ① ③ .
;20、 ① ③ .
24、已知直线l :kx-y+1=0,圆C:x2+y2-4x-5=0,
(1)求证:无论k取任何实数,直线l与圆C恒有两个不同的交点;
(2)当k=2时,直线l与圆C相交于A、B,求A、B两点间的距离;
(3)当实数k变化时,求直线l被圆C截得的弦的中点的轨迹方程.
解:(1)由直线l及圆C的方程消去y可得:(1+k2)x2+(2k-4)x-4=0①,(1¢)
∵D=(2k-4)2+16(1+k2)>0,(2¢)
∴对任意实数k,直线l与圆C有两个不同的交点;(3¢)
(2)经配方得,(x-2)2+y2=9,所以,
圆C的圆心C的坐标是(2,0),半径r=3,所以,当k=2时,
点C到直线l的距离为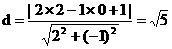 ,(5¢)
,(5¢)
故|AB|=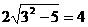 ;(6¢)
;(6¢)
(3)设两交点A、B的坐标分别为(x1,y1),(x2,y2),A、B的中点P的坐标分别为(x0,y0),(7¢)则
由①可得,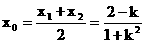 ②,(8¢)又由kx0-y0+1=0可得
②,(8¢)又由kx0-y0+1=0可得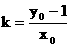 ③,(9¢)
③,(9¢)
将③代入②并化简可得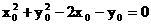 ,
,
故所求的轨迹方程为x2+y2-2x-y=0.(10¢)
第一学段模块考试
高一年级数学必修2试卷
高一数学第一模块结业考试试题(第Ⅱ卷)
23、 如图,DABC是直角三角形,ÐABC=900,AP^平面ABC,且AP=AB,点D是PB的中点,点E是PC上的一点,
如图,DABC是直角三角形,ÐABC=900,AP^平面ABC,且AP=AB,点D是PB的中点,点E是PC上的一点,
(1)当DE//BC时,求证:直线PB^平面ADE;
(2)当DE^PC时,求证:直线PC^平面ADE;
(3)当AB=BC时,求二面角A-PC-B的大小.
(1)证:∵AP=AB,点D是PB的中点,∴AD^PB,
∵AP^平面ABC,BCÌ平面ABC,
∴AP^BC,∵AB^BC,∴BC^平面PAB,
∵PBÌ平面PAB,∴BC^PB,
∵DE//BC,∴DE^PB,∴PB^平面ADE. (3¢)
(2)证:∵BC^平面PAB,ADÌ平面PAB,∴BC^AD,
又AD^PB,∴AD^平面PBC,∵PCÌ平面PBC,
∴AD^PC,
又DE^PC,∴PC^平面ADE. (6¢)
(3)由(2)可知,当DE^PC时,PC^平面ADE,
∴ÐAED是二面角A-PC-B的平面角. (7¢)
设AP=a,则AB=BC=a,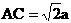 ,
,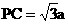 ,(8¢)
,(8¢)
∵AD^平面PBC,DEÌ平面PBC,∴AD^DE,
在RtDADE中,可求得,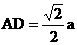 ,
,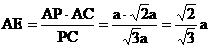 ,(9¢)
,(9¢)
∴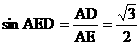 ,∴ÐAED=600,
,∴ÐAED=600,
∴二面角A-PC-B的大小为600. (10¢)
22、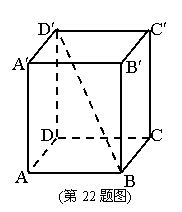 如图,在长方体AC¢中,已知底面两邻边AB和BC的长分别为3和4,对角线BD¢与平面ABCD所成的角为450,求:
如图,在长方体AC¢中,已知底面两邻边AB和BC的长分别为3和4,对角线BD¢与平面ABCD所成的角为450,求:
(1)长方体AC¢的高;
(2)长方体AC¢的表面积;
(3)几何体C¢D¢-ABCD的体积.
解:(1)连结BD,∵DD¢^平面ABCD,
∴Ð DBD¢是直线BD¢与平面ABCD所成的角.
∴Ð DBD¢=450,(2¢)∴DD¢= BD,
又AB=3,BC=4,∴DD¢= BD=5,
∴长方体AC¢的高为5.(4¢)
(2)长方体AC¢的表面积S=2(3´4+4´5+5´3)=94(平方单位)(7¢)
(3)几何体C¢D¢-ABCD的体积V=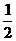 (3´4´5)=30(立方单位). (10¢)
(3´4´5)=30(立方单位). (10¢)
21、已知A(1,0)、B(0,1)、C(-3,-2)三点.
(1)试判断三角形ABC的形状;
(2)求三角形ABC的面积.
解:(1)kAB=-1,kBC=1,(2¢)kAB×kBC=-1,∴AB^BC,(4¢)
∴三角形ABC是直角三角形. (5¢)
(2)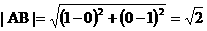 ,
,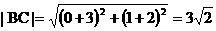 (8¢)
(8¢)
∴三角形ABC的面积为
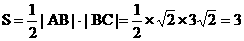 (平方单位). (10¢)
(平方单位). (10¢)
20、已知直线a、b及平面a,在下列命题:
①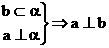 ;②
;②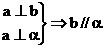 ;③
;③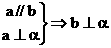 ;④
;④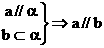
中,正确的有 ① ③ (只填序号).
19、已知三棱柱ABC-A´B´C´所有的棱长均为2,且侧棱与底面垂直,则该三棱柱的体积是 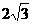 (立方单位);
(立方单位);
18、以点C(-1,2)为圆心且与x轴相切的圆的方程为(x+1)2+(y-2)2=4;
17、两平行直线4x-3y+3=0和4x-3y-7=0之间的距离为__ 2 _____;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com