
题目列表(包括答案和解析)
18.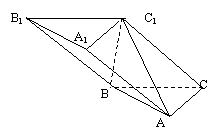 如图,斜三棱柱ABC-A1B1C1中,A1C1⊥BC1,AB⊥AC,AB=3,AC=2,侧棱与底面成60°角。
如图,斜三棱柱ABC-A1B1C1中,A1C1⊥BC1,AB⊥AC,AB=3,AC=2,侧棱与底面成60°角。
(1)求证:AC⊥面ABC1;
(2)求证:C1点在平面ABC上的射影H在直线AB上;
(3)求此三棱柱体积的最小值。
17.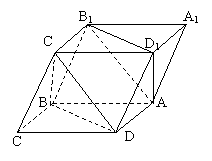 已知:平行六面体
已知:平行六面体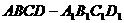 的底面ABCD是菱形,且满足:
的底面ABCD是菱形,且满足: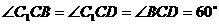
(1)面C1BD//面AB1D1
(2)证明 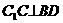 ;
;
(3)当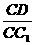 的值为多少时,能使
的值为多少时,能使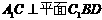 ?请给出证明.
?请给出证明.
16.设集合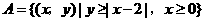 ,
,
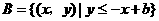 ,
,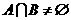 ,
,
(1)画出集合A表示的图形,并求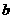 的取值范围;
的取值范围;
(2)若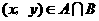 ,且S=
,且S=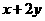 的最大值为9,求
的最大值为9,求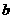 的值.
的值.
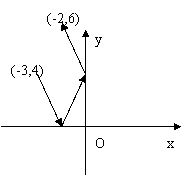
15.一条光线从点A(-3,4)发出,经过x轴反射,又经过y轴反射后过点 B(-2,6),
(1)求过点B的反射光线所在直线的方程;
(2)求过点A的入射光线与过点B的的反射光线所在直线间的距离。
14. 无盖的圆柱形容器的底面半径为1,母线长为3,现将盛满水的该容器平稳地缓慢倾斜,当倒出的水是原来的
无盖的圆柱形容器的底面半径为1,母线长为3,现将盛满水的该容器平稳地缓慢倾斜,当倒出的水是原来的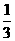 时,圆柱母线与水平面所成的角为________。
时,圆柱母线与水平面所成的角为________。
13.已知{an}是等差数列,公差d不为零,它的前n项和为Sn,设集合A={(an, 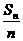 )| n∈N+},若以A中的元素作为点的坐标,这些点都在同一直线上,则这条直线的斜率为_________
)| n∈N+},若以A中的元素作为点的坐标,这些点都在同一直线上,则这条直线的斜率为_________
12. 已知直线m、n及平面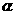 ,其中m∥n,那么在平面
,其中m∥n,那么在平面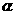 内到两条直线m、n距离相等的点的集合可能是:①一条直线;②整个平面;③一个点;④空集.其中正确命题的序号是
.
内到两条直线m、n距离相等的点的集合可能是:①一条直线;②整个平面;③一个点;④空集.其中正确命题的序号是
.
11. OX,OY,OZ是空间交于同一点O的互相垂直的三 条直线,点P到这三条直线的距离分别为3,4,7,则OP长为_______.
10. 在直四棱柱ABCD-A1B1C1D1中,当底面四边形ABCD满足条件
时,有A1C⊥ B1D1(注:填上你认为正确的一种即可,不必考虑所有可能的情形).
在直四棱柱ABCD-A1B1C1D1中,当底面四边形ABCD满足条件
时,有A1C⊥ B1D1(注:填上你认为正确的一种即可,不必考虑所有可能的情形).
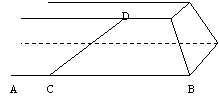
9. 河堤斜面与水平面所成角为60°,河堤斜面上有一条直道CD,它与 水平线AB的夹角为30°,沿着这条直道从点C向上行走10米时,人相对于水平面升高了多少______米。(精确到0.1)
 (
(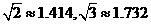 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com