
题目列表(包括答案和解析)
7 已知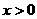 且
且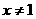 ,
,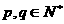 ,则
,则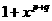 与
与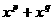 的大小关系是
的大小关系是
8 已知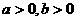 ,且
,且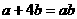 ,则
,则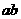 的最小值是
的最小值是
9 正数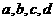 满足
满足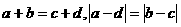 ,则
,则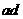 与
与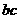 的大小关系是
的大小关系是
10 给出下列不等式: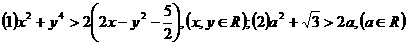 ;
;
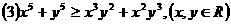 ,其中正确不等式的序号是
,其中正确不等式的序号是
1 设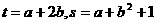 ,则
,则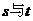 的大小关系是
( )
的大小关系是
( )
A 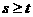 B
B 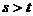 C
C
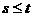 D
D 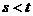
2 设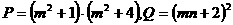 ,则 ( )
,则 ( )
A 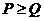 B
B 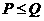 C
C 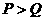 D
D 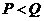
3 若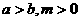 ,则下列不等式恒成立的是
( )
,则下列不等式恒成立的是
( )
A 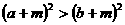 B
B

C 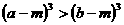 D
D
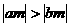
4 若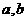 均为正数,
均为正数,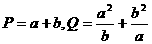 ,则
,则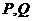 的关系为
( )
的关系为
( )
A 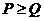 B
B 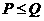 C
C 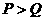 D
D 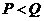
5 下列不等式中,恒成立的是 ( )
A 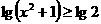 B
B 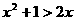 C
C 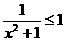 D
D 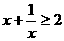
6 若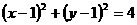 ,则
,则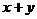 的取值范围是
( )
的取值范围是
( )
A 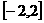 B
B 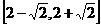 C
C 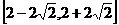 D
D 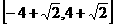
19、(14分)若非零函数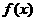 对任意实数
对任意实数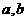 均有
均有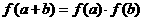 ,且当
,且当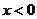 时,
时,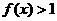 ;
;
(1)求证: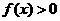 (2)求证:
(2)求证: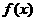 为减函数
为减函数
(3)当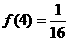 时,解不等式
时,解不等式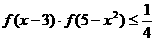
附加题:(10分)
请自行设计一个盛水容器(画出大致形状),并在容器右侧作出向容器中匀速注水时,水深h关于注水量V(或注水时间t)函数的大致图象.
18、(10分)快艇和轮船分别从A地和C地同时开出,如下图,各沿箭头方向航行,快艇和轮船的速度分别是45 km/h和15 km/h,已知AC=150km,经过多少时间后,快艇和轮船之间的距离最短?
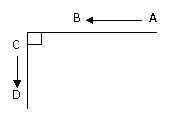
17、(10分)在水果产地批发水果,100kg为批发起点,每100kg40元;100至1000kg8折优惠;1000kg至5000kg,超过1000部分7折优惠;5000kg至10000kg,超过5000kg的部分6折优惠;超过10000kg,超过部分5折优惠。
(1)请写出销售额y与销售量x之间的函数关系;
(2)某人用2265元能批发多少这种水果?
16、(10分)设函数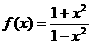 .
.
1 求它的定义域;2 判断它的奇偶性;3 求证: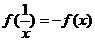 .
.
15.(10分)判断函数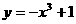 的单调性并证明你的结论.
的单调性并证明你的结论.
14、已知函数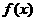 的图象关于直线
的图象关于直线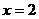 对称,且在区间
对称,且在区间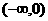 上,当
上,当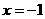 时,
时,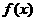 有最小值3,则在区间
有最小值3,则在区间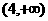 上,当
上,当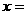 ____时,
____时,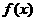 有最____值为_____.
有最____值为_____.
13、若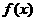 是一次函数,
是一次函数,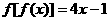 且,则
且,则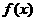 = _________________.
= _________________.
12、已知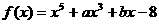 且
且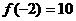 ,那么
,那么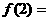
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com