
题目列表(包括答案和解析)
5.若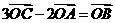 ,则
,则
A.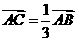 B.
B.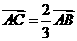 C.
C.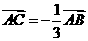 D.
D.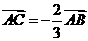
4.若角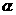 的终边落在直线
的终边落在直线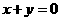 上,则
上,则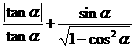 的值等于
的值等于
A.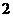 或
或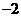 B.
B.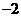 或
或 C.
C. D.
D. 或
或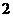
3.在下列函数中,既不是奇函数又不是偶函数的是
A.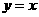 B.
B.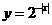 C.
C.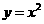 D.
D.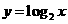
2.设函数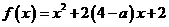 在区间
在区间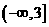 上是减函数,则实数
上是减函数,则实数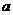 的取值范围是
的取值范围是
A.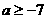 B.
B.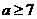 C.
C.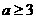 D.
D.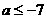
1. 设集合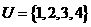 ,
,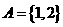 ,
,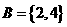 ,则
,则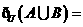
|
命题人 |
|
杨彦平 |
|
审核人 |
|
李茂生 |
A.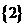 B.
B.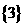 C.
C.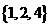 D.
D.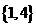
21. (本题14分)通常用a、b、c表示△ABC的三个内角∠A、∠B、∠C所对边的边长, R表示△ABC外接圆半径.
(1) 如图所示, 在以O为圆心, 半径为2的⊙O中, BC和BA是⊙O的弦, 其中BC=2, ∠ABC=45°, 求弦AB的长;
(2) 在△ABC中, 若∠C是钝角, 求证: a2+b2<4R2;
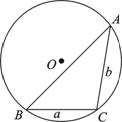 (3) 给定三个正实数a、b、R, 其中b≤a, 问:a、b、R满足怎样的关系时, 以a、b为边长, R为外接圆半径的△ABC不存在, 存在一个或两个(全等的三角形算作同一个)? 在△ABC存在的情况下, 用a、b、R表示c.
(3) 给定三个正实数a、b、R, 其中b≤a, 问:a、b、R满足怎样的关系时, 以a、b为边长, R为外接圆半径的△ABC不存在, 存在一个或两个(全等的三角形算作同一个)? 在△ABC存在的情况下, 用a、b、R表示c.
武汉二中2009-2010学年上学期
20. (本题13分)已知函数f (x)=4sinx·sin2(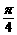 +
+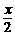 )+2cos2x+1+a,
x
)+2cos2x+1+a,
x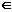 R是一个奇函数.
R是一个奇函数.
(1) 求a的值和f (x)的值域;
(2) 设w>0, 若y=f
(wx)在区间[-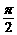 ,
, 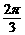 ]的增函数, 求w的取值范围;
]的增函数, 求w的取值范围;
(3) 设|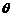 |<
|<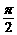 , 若对x取一切实数, 不等式4+f (x+
, 若对x取一切实数, 不等式4+f (x+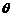 )f (x-
)f (x-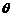 )>2f (x)都成立,
)>2f (x)都成立,
求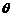 的取值范围.
的取值范围.
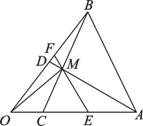
19. (本题12分)如图所示, 在△ABC中, 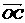 =
=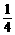
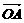 ,
, 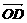 =
=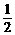
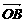 , AD与BC交于M点.
, AD与BC交于M点.
 设
设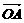 =a,
=a, 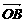 =b,
=b,
(1) 用a, b表示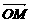 ;
;
(2) 在已知线段AC上取一点E, 在线段BD上取一点F,
使EF过点M, 设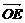 =p
=p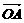 ,
, 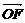 =q
=q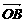 , 求
, 求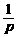 +
+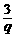 的值.
的值.
18. (本题12分) 设向量a=(4cos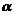 , sin
, sin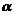 ), b=(sin
), b=(sin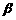 , 4cos
, 4cos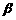 ), c=(cos
), c=(cos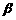 , -4sin
, -4sin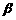 ).
).
(1) 若a与b-2c垂直, 求tan(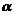 +
+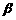 )的值;
)的值;
(2) 求|b+c|的最大值;
(3) 若tan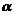 ·tan
·tan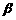 =16, 求证: a∥b.
=16, 求证: a∥b.
17.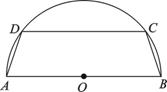 (本题12分)有一块半径为2的半圆形钢板, 计划剪裁成等腰梯形ABCD的形状, 它的下底AB是⊙O的直径, 上底CD的端点在圆周上.
(本题12分)有一块半径为2的半圆形钢板, 计划剪裁成等腰梯形ABCD的形状, 它的下底AB是⊙O的直径, 上底CD的端点在圆周上.
(1) 当腰长为1, 求等腰梯形周长;
(2) 设等腰梯形ABCD周长为y, 求y的最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com