
题目列表(包括答案和解析)
4. 如图,在一个边长为3cm的正方形内部画一个边长为2cm的小正方形,向大正方形内随机投点,则所投点落在小正方形内的概率是 ▲ .
3. 口袋中有若干白球、红球和黄球,已知摸出白球的概率是0.35,摸出红球的概率是0.43,则摸出黄球的概率是 ▲ .
2. 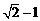 和
和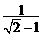 的等差中项是 ▲ .
的等差中项是 ▲ .
1. 某林场有树苗30 000棵,其中松树苗4 000棵. 为调查树苗的生长情况,采用分层抽样的方法抽取一个容量为150的样本,则样本中松树苗的数量为 ▲ .
20.(本题满分16分)
设正项等差数列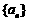 的前n项和为
的前n项和为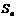 ,其中
,其中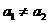 .
.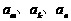 是数列
是数列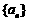 中满足
中满足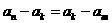 的任意项.
的任意项.
(1)求证: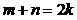 ;
;
(2)若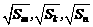 也成等差数列,且
也成等差数列,且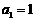 ,求数列
,求数列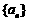 的通项公式;
的通项公式;
(3)求证: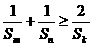 .
.
海门市2009-2010学年度第二学期期末考试
19.(本题满分16分)
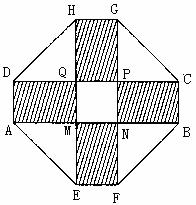
 2010年上海世博会某国要建一座八边形的展馆区,它的主体造型的平面图是由两个相同的矩形
2010年上海世博会某国要建一座八边形的展馆区,它的主体造型的平面图是由两个相同的矩形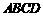 和
和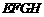 构成的面积为200
构成的面积为200 的十字型地域,计划在正方形
的十字型地域,计划在正方形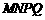 上建一座“观景花坛”,造价为4200元
上建一座“观景花坛”,造价为4200元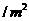 ,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元
,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元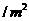 ,再在四个空角(如
,再在四个空角(如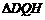 等)上铺草坪,造价为80元
等)上铺草坪,造价为80元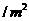 .设
.设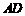 长为
长为 ,
,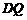 长为
长为 .
.
(1)试找出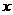 与
与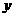 满足的等量关系式;
满足的等量关系式;
(2)设总造价为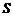 元,试建立
元,试建立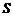 与
与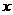 的函数关系;
的函数关系;
(3)若总造价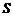 不超过138000元,求
不超过138000元,求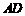 长
长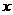 的取值范围.
的取值范围.
18.(本题满分15分)
已知数列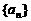 满足:
满足: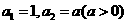 ,数列
,数列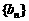 满足
满足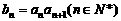 .
.
(1)若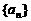 是等差数列,且
是等差数列,且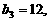 求
求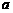 的值及
的值及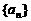 的通项公式;
的通项公式;
(2)若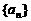 是等比数列,求
是等比数列,求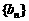 的前
的前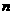 项和
项和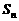 ;
;
(3)若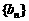 是公比为
是公比为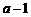 的等比数列,问是否存在正实数
的等比数列,问是否存在正实数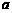 ,使得数列
,使得数列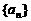 为等比数列?若存在,求出
为等比数列?若存在,求出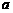 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
17.(本题满分15分)
在平面直角坐标系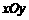 中,点
中,点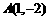 ,
,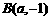 ,
,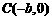 ,且
,且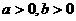 .
.
(1)若点 、
、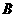 、
、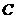 在直线
在直线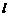 上,求
上,求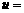
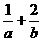 的最小值,并求此时直线
的最小值,并求此时直线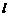 的方程;
的方程;
(2)若以线段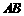 、
、 为邻边的平行四边形两条对角线的长相等,且
为邻边的平行四边形两条对角线的长相等,且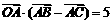 ,求
,求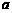 、
、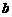 的值.
的值.
16.(本题满分14分)
“根据《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在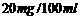 -
-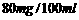 (不含80)之间,属于酒后驾车,血液酒精浓度在
(不含80)之间,属于酒后驾车,血液酒精浓度在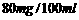 (含80)以上时,属醉酒驾车.”
(含80)以上时,属醉酒驾车.”
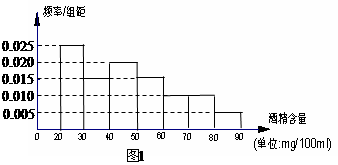
某晚某市交警大队在该市一交通岗前设点对过往的车辆进行抽查,经过两个小时共查出血液酒精浓度不低于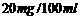 驾车者40名,图1是这40 名驾车者血液酒精浓度结果的频率分布直方图.
驾车者40名,图1是这40 名驾车者血液酒精浓度结果的频率分布直方图.
 (1)求这40名驾车者中属酒后驾车的人数;(图1中每组包括左端点,不包括右端点)
(1)求这40名驾车者中属酒后驾车的人数;(图1中每组包括左端点,不包括右端点)
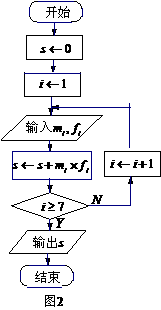
(2)统计方法中,同一组数据常用该组区间的中点值(组中值)作为代表,图2的程序框图是对这40名驾车者血液的酒精浓度做进一步的统计.求图2输出的S值;(图2中数据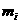 与
与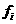 分别表示图1中各组的组中值及频率)
分别表示图1中各组的组中值及频率)
(3)本次行动中,吴、李两位先生都被酒精测试仪测得酒精浓度属于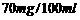 -
-
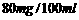 的范围,但他俩坚称没喝那么多,是测试仪不准,交警大队王队长决定在被酒精测试仪测得酒精浓度属于
的范围,但他俩坚称没喝那么多,是测试仪不准,交警大队王队长决定在被酒精测试仪测得酒精浓度属于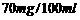 -
-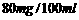 范围的驾车者中随机抽出2人抽血检验,则吴、李两位先生至少有1人被抽中的概率为 ▲ .
范围的驾车者中随机抽出2人抽血检验,则吴、李两位先生至少有1人被抽中的概率为 ▲ .
15.(本题满分14分)
 中,角
中,角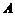 、
、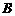 、
、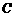 的对边分别为
的对边分别为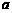 、
、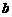 、
、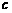 ,且
,且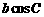 ,
, ,
, 成等差数列.
成等差数列.
(1)求角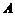 的大小;
的大小;
(2)若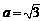 ,
,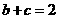 ,求
,求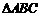 的面积.
的面积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com