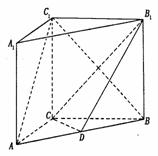
21．(1)证明：正方形ABCD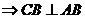　 ∵面ABCD⊥面ABEF且交于AB，

∴CB⊥面ABEF　 ∵AG，GB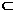面ABEF，　 ∴CB⊥AG，CB⊥BG

又AD=2a，AF= a，ABEF是矩形，G是EF的中点，

∴AG=BG=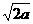，AB=2a， AB²=AG²+BG²，∴AG⊥BG ∵CG∩BG=B ∴AG⊥平面CBG　 而AG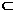面AGC，　 故平面AGC⊥平面BGC　

　 (2)解：如图，由(Ⅰ)知面AGC⊥面BGC，且交于GC，在平面BGC内作BH⊥GC，垂足为H，则BH⊥平面AGC，　　 ∴∠BGH是GB与平面AGC所成的角

∴在Rt△CBG中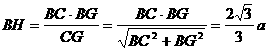　　 又BG=，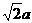

∴

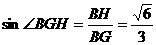
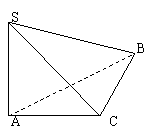
20．解：(1)∵∠SAB=∠SCA=90⁰

(2)

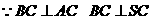
19．略

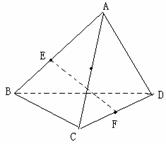
18．，解：(1)连CE、DE，在等边△ABC中，EC=DE=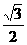a，

　　　　 ∴EF是等腰△ECD底边上的高，EF⊥CD，

　　　　 EF=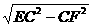=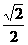a

　　 (2)方法一：

　　　 取BC中点G，连AG、DG，易知BC⊥AG、BC⊥DG，

∴BC⊥面AGD，则BC⊥AD，∴BC，AD所成角为90⁰，

方法二：

取AC中点H，连EH、FH，则θ=∠EHF是BC、AD所成的角，

　　　　 由余弦定理得cosθ=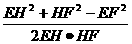=0，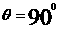

17．解：圆锥的高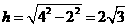，圆柱的底面半径，

　　　　 表面积：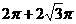

圆锥体积：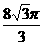

13、　 8　　 14、　 7　 15、　 4　 16、(1)(3)(4)

1~6。DACDBA　　　 7~12。DADACD

17题：

18题：

19题：

20题：

21题：

22题：

答案(供稿)

15、＿＿＿＿＿　　　　　　 　　　16、＿＿＿＿＿

13、＿＿＿＿＿＿　　　　　　　 14、＿＿＿＿＿＿