
题目列表(包括答案和解析)
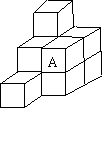
9. 把10个相同的小正方体,按如图所示的位置堆放,它的外表含有若干小正方形.如果将图中标有A的一个小正方体搬去,这时外表含有的小正方形个数与搬去前相比
A.不增不减 B.减少1个 C.减少2个
D.减少3个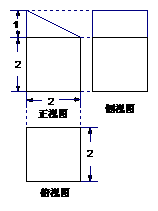
8.已知直线 、
、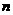 ,平面
,平面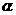 、
、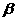 ,给出下列命题:
,给出下列命题:
①若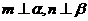 ,且
,且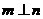 ,则
,则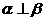 ②若
②若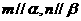 ,且
,且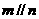 ,则
,则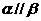
③若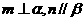 ,且
,且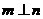 ,则
,则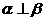 ④若
④若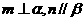 ,且
,且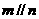 ,则
,则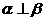
其中正确的命题是
 A.②③ B.①③ C.①④ D.③④
A.②③ B.①③ C.①④ D.③④
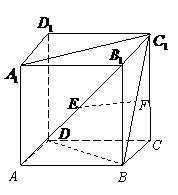
7.如图,在正方体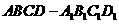 中,
中,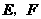 分别
分别
是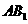 ,
,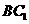 的中点,则以下结论中不成立的是
的中点,则以下结论中不成立的是
A. 与
与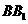 垂直 B.
垂直 B. 与
与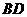 垂直
垂直
C. 与
与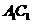 异面 D.
异面 D.  与
与 异面
异面
6.正四面体 中,
中,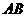 与平面
与平面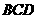 所成角的正弦值为
所成角的正弦值为
 A.
A.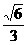
 B.
B.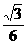 C.
C.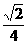 D.
D. 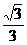
5.四棱台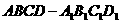 的12条棱中,与棱
的12条棱中,与棱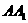 异面的棱共有
异面的棱共有
A.3条 B.4条 C.6条 D.7条
4.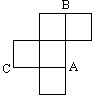 如图,是一个无盖的正方体盒子展开后的平面图,
如图,是一个无盖的正方体盒子展开后的平面图,  、
、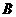 、
、 是展
是展
开图上的三点, 则正方体盒子中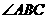 的值为
的值为
A.
 B.
B.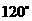 C.
C.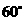 D.
D.
3.棱长为2的正方体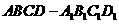 中,
中,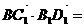
A.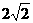
 B.
B.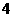 C.
C.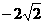 D.
D.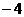
2.在空间中,垂直于同一直线的两条直线的位置关系是
A.垂直 B.平行 C.异面 D.以上都有可能
1.已知正方体的棱长为2,则其外接球的半径为
A.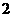 B.
B.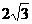 C.
C.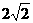 D.
D.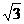
22.方法一:(1)证明: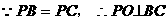
又 平面
平面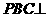 平面ABCD
平面ABCD
平面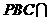 平面ABCD=BC,
平面ABCD=BC,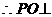 平面ABCD ……2分
平面ABCD ……2分
在梯形ABCD中,可得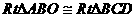
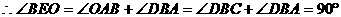 ,即
,即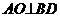
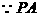 在平面ABCD内的射影为AO,
在平面ABCD内的射影为AO,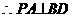 ……4分
……4分
(2)解: ,且平面
,且平面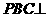 平面ABCD
平面ABCD
∴DC⊥平面PBC 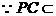 平面PBC,
平面PBC,
∴∠PCB为二面角P-DC-B的平面角 ……6分
∵△PBC是等边三角形,∴∠PCB=60°,即二面角P-DC-B的大小为60° ……8分
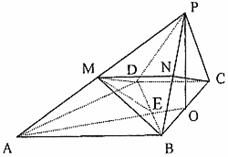 (3)证明:取PB的中点N,连结CN
(3)证明:取PB的中点N,连结CN
∵PC=BC,∴CN⊥PB ①
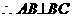 ,且平面
,且平面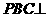 平面ABCD
平面ABCD
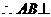 平面PBC ……………10分
平面PBC ……………10分
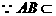 平面PAB
平面PAB  平面
平面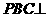 平面PAB ②
平面PAB ②
由①、②知CN⊥平面PAB
连结DM、MN,则由MN∥AB∥CD
 MN=AB=CD,得四边形MNCD为平行四边形
MN=AB=CD,得四边形MNCD为平行四边形
∴CN∥DM
∴DM⊥平面PAB
∵DMÌ平面PAD  平面PAD⊥平面PAB ………………12分
平面PAD⊥平面PAB ………………12分
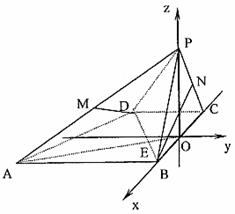
方法二:取BC的中点O,因为△PBC是等边三角形,
由侧面PBC⊥底面ABCD 得PO⊥底面ABCD ……1分
以BC中点O为原点,以BC所在直线为x轴,过点O与
AB平行的直线为y轴,建立如图所示的空间直角坐标系
O-xyz……2分
(1)证明:∵CD=1,则在直角梯形中,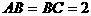
在等边三角形PBC中,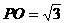
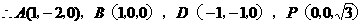
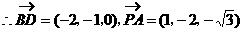
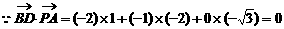
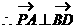 ,即
,即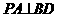 ……4分
……4分
(2)解:取PC中点N,则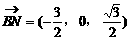

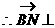 平面PDC,显然
平面PDC,显然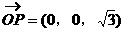 ,且
,且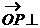 平面ABCD
平面ABCD
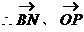 所夹角等于所求二面角的平面角 ……6分
所夹角等于所求二面角的平面角 ……6分
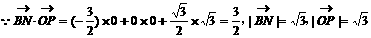
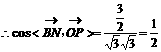
 二面角
二面角 的大小为
的大小为 ……8分
……8分
(3)证明:取PA的中点M,连结DM,则M的坐标为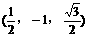
又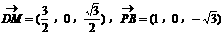 ……10分
……10分
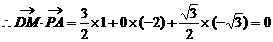
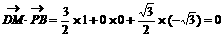
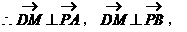 即
即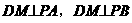
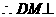 平面PAB,
平面PAB, 平面
平面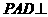 平面PAB.
平面PAB.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com