
题目列表(包括答案和解析)
20.依题意四面体P-ABC中,∠APB=∠BPC=∠CPA=90°,设PA=x,PB=y,PC=z.
则AC=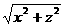 ,BC=
,BC=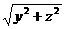 ,AB=
,AB=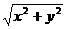 …………2分
…………2分
∵PA、PB、PC两两垂直 ∴VP-ABC=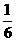 xyz ∴a=PA+PB+PC+AB+BC+CA
xyz ∴a=PA+PB+PC+AB+BC+CA
=x+y+z+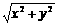 +
+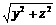 +
+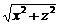 …………4分 ≥3
…………4分 ≥3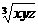 +
+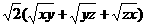 ≥3
≥3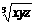 +3
+3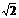
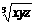
=3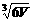 +3
+3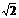
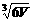 …………7分 ∴
…………7分 ∴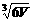 ≤
≤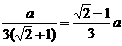
∴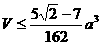 当且仅当x=y=z时,上式等号成立.
当且仅当x=y=z时,上式等号成立.
即A、B、C三点距P点距离为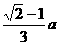 时四面体有最大体积
时四面体有最大体积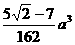 ……………………10分
……………………10分
19.①过P在平面PCD内作PO⊥CD,垂足为O,∵△PCD为正三角形 ∴O为CD的中点
又平面PCD⊥底面ABCD ∴PO⊥底面ABCD 而ABCD为菱形,由面积得
2·2sin∠ADC=2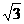
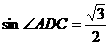 ∴∠ADC=60°
∴∠ADC=60°
从而△ACD为正三角形,AO⊥CD,∴PA⊥CD……………………………6分
②设过C、D、M的平面交PA于N,∵CD//AB ∴CD//平面PAB ∴CD//MN//AB
由于M为PB的中点,∴N为PA的中点. 又PD=AD ∴DN⊥PA 由①可知PA⊥CD
∴PA⊥平面CDM 于是平面CDM⊥平面PAB…………………………10分
18.①由题设可知△ABC为等腰直角三角形,∴∠ACD=90° 即AC⊥CD ∵平面ABC⊥平面ACD∴CD⊥平面ABC 于是CD⊥AB 又AB⊥BC ∴AB⊥平面BCD…3分
②过B在平面ABC内作BO⊥AC,垂足为O,∵平面ABC⊥平面ACD,∴BO⊥平面ACD在平面ACD内作OE⊥AD,垂足为E,连结BE,则BE⊥AD ∴∠BEO为平面ABD与平面ACD所成二面角的平面角. 在Rt△BEO中,BO=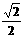 a,由
a,由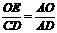 得
得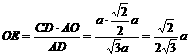 于是
于是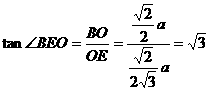
∴∠BEO=60°…………7分
③设C到平面ABD的距离为h,由VC-ABD=VB-ACD 得 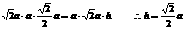 …10分
…10分
17.设多面体的顶点数为V,棱数为E,面数为F ∵每个面都是五边形,∴每个面都有五条棱故E=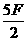 F=
F=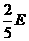 …………3分 又每个顶点都有三条棱相交,∴E=
…………3分 又每个顶点都有三条棱相交,∴E=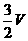 V=
V=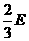 …………6分
…………6分
由欧拉公式 V+F-E=2得 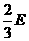 +
+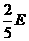 -E=2 解得 E=30 F=12,V=20……8分
-E=2 解得 E=30 F=12,V=20……8分
16.假设H是△SBC的垂心,连接BH,则BH⊥SC………………………………2分
而BH为AB在平面SBC内的射影. ∴BH⊥AB 又SA⊥底面ABC ∴SA⊥AB 于是AB⊥平面SAC………………6分 ∴AB⊥AC 即∠BAC=90°
这与△ABC是锐角三角形矛盾,故假设不成立,H不可能是△SBC的垂心.……8分
20.(本小题满分10分)用总长为a米的钢条,制成一个顶点P的三个角都是直角的四面体P-ABC的六条棱,问截面ABC的位置怎样时,所围成的四面体的体积最大?
棱 锥
19.(本小题满分10分)四棱锥P-ABCD中,侧面PDC是边长为2的正三角形,且与底面垂直,底面ABCD是面积为2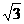 的菱形,∠ADC为锐角,M为PB的中点.
的菱形,∠ADC为锐角,M为PB的中点.
①求证:PA⊥CD;②求证:平面CDM⊥平面PAB.
18.(本小题满分10分)在平面四边形ABCD中,AB=BC=CD=a,
∠B=90°,∠C=135°,沿对角线AC将△ABC折起,使二面角B-AC-D成直二面角.
①求证:AB⊥平面BCD;
②求平面ABD与平面ACD所成二面角的大小;③求C到平面ABD的距离.
17.(本小题满分8分)已知简单多面体的每个面都是五边形,每个顶点都有3条棱相交,试求多面体的顶点数,棱数和面数.
16.(本小题满分8分)在三棱锥S-ABC中,SA⊥底面ABC.△ABC是锐角三角形,H是A在平面SBC内的射影.求证:H不可能是△SBC的垂心.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com