
题目列表(包括答案和解析)
4.实数方程(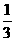 )x=x
)x=x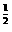 的解的个数是( )
的解的个数是( )
A.1个 B.2个 C.3个 D.4个
3.函数f(x)=lg(x-2)+(x-3)0的定义域是( )
A.{x|x>2}
B.{x|x>3}
C.{x|x>2或x≠3}
D.{x|x>2且x≠3}
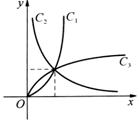
2.图中的曲线是亲函数y=xn在第一象限内的图象,已知n取2,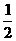 ,-1三个值,则曲线C1、C2、C3的n值依次为( )
,-1三个值,则曲线C1、C2、C3的n值依次为( )
A.2,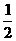 ,-1
,-1
B.-1,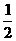 ,2
,2
C.2,-1,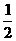
D.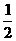 ,2,-1
,2,-1
1.下列函数表达式中表不幂函数的是( )
A.y=2x3
B.y=x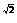
C.y=-x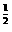
D.y=πx
19.某饭店白助厅每消费一次收费10元,每消费满10次送2次免费.
(1)某客户累计消费54次,共交费多少元?
(2)某客户累计消费n次,共交费y元,写出y与n的函数关系式.
答案:(1)消费54次共花费460元
(2)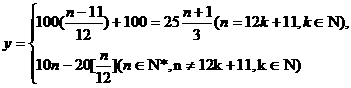
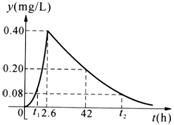
18.某口服抗生素做药物代谢动力学实验:服药后能快速被血液吸收,2.6 h后,血液药浓度达到峰值0.40 mg/L,单剂给药血消除半衰期39.4 h(从峰值到一半的时间),设t(h)为服药后的时间,y(mg/L)表示血液药浓度,拟合函数关系为:
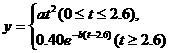 (如图).
(如图).
(1)求函数的表达式;
(2)血液中药浓度不低于0.08mg/L对细菌有抑制作用,求下一次服药的时间t.
答案:(1)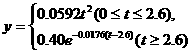
(2)t2≈94 h
17.已知函数f(x)=lnx,g(x)=4-x,并且给定了部分数据如下表:
|
x |
0.5 |
0.74 |
1.5 |
2.6 |
2.7 |
2.75 |
2.8 |
2.9 |
3 |
|
lnx |
-0.69 |
-0.29 |
0.41 |
0.96 |
0.99 |
1.01 |
1.02 |
1.06 |
1.10 |
(2)利用图象求方程lnx=4-x的近似解(精确到0.1).
答案:(1)图象略
(2)方程lnx=4-x的近似解为2.9
16.人体的代谢率的变化随人的生活环境温度的变化而改变.下表是由实验得到的人体代谢率y(4 185 J/(h.m2))与环境温度t(℃)的部分对应数据,已知函数图象为折线.
|
环境温度℃ |
4 |
10 |
20 |
30 |
38 |
|
代谢率(4185 J/(h.m2)) |
60 |
44 |
40 |
40.5 |
54 |
(1)在右下图的坐标系中描绘函数图象,
(2)当温度在什么范围时,代谢率较低,并且较稳定?
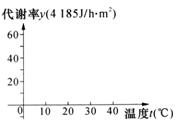
答案:(1)函数图象如右图
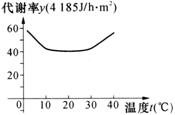
(2)当温度在20-30℃时代谢最低
演算步骤)
15.用二分法求方程2x2+3x-3=0的一个实数解.(精确到0.1)
答案:设f(x)-2x3+3x-3,∵f(0)=-3<0,f(1)=2>0,∴方程f(x)=0的根在(0,1)内,令x1=0.5,∵f(0.5)=-1.25<0,∴方程f(x)=0的根在(0.5,1)内;…令x4=0.687 5,∵f(0.687 5)≈-0.287<0,f(0.75)≈0.094>0,∴方程f(x)=0的根在(0.687 5,0.75);令x5=0.718 75,∵(0.718 75)≈-0.101<0,∴方程f(x)=0的根在(0.718 75,0.75);令x6=0.734 375,∵f(0.734 375)<0,∴方程f(x)=0的根在(0.734 375,0.75);令x7=0.742 187 5,∵f(0.742 187 5)≈0.044>0,∴方程f(x)=0的根在(0.734 375,0.742 187 5).∵区间(0.734 375,0.742 187 5)的两个端点值精确到0.1的近似值都是0.7, ∴0.7是方程的一个近似解
14.上世纪末我国高速公路通车总里程以年平均47.8%的增长率递增,若1996年底,通车总里程为3 422 km,则2000底,通车总里程约为__________km(结果保留整数)
答案:16 330
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com