9．(10分)已知点(，2)在幂函数f(x)的图象上，点

在幂函数g(x)的图象上，当x为何值时：

(1)f(x)>g(x)；(2)f(x)＝g(x)；(3)f(x)<g(x)．

[解析]　根据幂函数的概念，利用待定系数法求出幂函数的解析式，再结合图象确定满足条件的x的取值范围．

设f(x)＝x^α，则()^α＝2，得α＝2，所以f(x)＝x²；同理可得g(x)＝x^－1.

在同一直角坐标系内作出函数

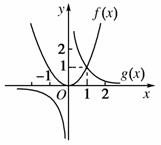
f(x)=x2与g(x)=x-1的图象(如图所示)，由图象可知：

(1)当x<0或x>1时，f(x)>g(x)；

(2)当x=1时，f(x)=g(x)；

(3)当0<x<1时，f(x)<g(x)．

8．已知幂函数y＝x^p－3(p∈N^*)的图象关于y轴对称，且在

(0，+∞)上是减函数，求满足(a－1)<(3+2a)的a的取值范围．

[解析]　∵函数y＝x^p－3在(0，+∞)上是减函数，

∴p－3<0，即p<3，又∵p∈N^*，∴p＝1，或p＝2.

∵函数y＝x^p－3的图象关于y轴对称，

∴p－3是偶数，∴取p＝1，即y＝x^－2，(a－1)<(3+2a)

∵函数y＝x在(－∞，+∞)上是增函数，

∴由(a－1)<(3+2a)，得a－1<3+2a，即a>－4.

∴所求a的取值范围是(－4，+∞)．

7．已知f(x)＝，

(1)判断f(x)在(0，+∞)上的单调性并证明；

(2)当x∈[1，+∞)时，求f(x)的最大值．

[解析]　函数f(x)在(0，+∞)上是减函数．

证明如下：

任取x₁、x₂∈(0，+∞)，且x₁<x₂，

f(x₁)－f(x₂)＝－＝＝

∵0<x₁<x₂，∴x₁+x₂>0，x₂－x₁>0，x₁²x₂²>0.

∴f(x₁)－f(x₂)>0，即f(x₁)>f(x₂)．

∴函数f(x)在(0，+∞)上是减函数．

(2)由(1)知，f(x)的单调减区间为(0，+∞)，

∴函数f(x)在[1，+∞)上是减函数，

∴函数f(x)在[1，+∞)上的最大值为f(1)＝2.

6．设f(x)＝(m－1)xm²－2，如果f(x)是正比例函数，则m＝________，如果f(x)是反比例函数，则m＝________，如果f(x)是幂函数，则m＝________.

[解析]　f(x)＝(m－1)xm²－2，

若f(x)是正比例函数，则∴m＝±；

若f(x)是反比例函数，则即∴m＝－1；

若f(x)是幂函数，则m－1＝1，∴m＝2.

[答案]　±　－1　2

5．已知n∈{－2，－1,0,1,2,3}，若ⁿ>ⁿ，则n＝________.

[解析]　∵－<－，且ⁿ>ⁿ，

∴y＝xⁿ在(－∞，0)上为减函数．

又n∈{－2，－1,0,1,2,3}，

∴n＝－1或n＝2.

[答案]　－1或2

4．已知幂函数y＝f(x)的图象经过点，则f(4)的值为(　)

A．16　 B．2

C.　 D.

[解析]　设f(x)＝x^α，则2^α＝＝2－，所以α＝－，f(x)＝x－，f(4)＝4－＝.故选C.

[答案]　C

3．设α∈{－1,1，，3}，则使函数y＝x^α的定义域为R且为奇函数的所有α的值为(　)

A．1,3　 B．－1,1

C．－1,3　 D．－1,1,3

[解析]　y＝x^－1＝的定义域不是R；y＝x＝的定义域不是R；y＝x与y＝x³的定义域都是R，且它们都是奇函数．故选A.

[答案]　A

2.

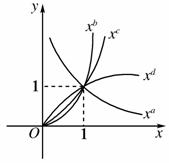
幂函数y=xa，y=xb，y=xc，y=xd在第一象限的图象如图所示，则a，b，c，d的大小关系是(　)

A．a>b>c>d

B．d>b>c>a

C．d>c>b>a

D．b>c>d>a

[解析]　由幂函数的图象及性质可知a<0，b>c>1,0<d<1，

∴b>c>d>a.故选D.

[答案]　D

1．T₁＝，T₂＝，T₃＝，则下列关系式正确的是(　)

A．T₁<T₂<T₃　 B．T₃<T₁<T₂

C．T₂<T₃<T₁　 D．T₂<T₁<T₃

[解析]　构造函数y＝x，此函数在[0，+∞)上是增函数，

则>，

即T₂<T₁，构造函数y＝^x，

此函数在R上是减函数，

则<，即T₁<T₃，

∴T₂<T₁<T₃.故选D.

高·考￥资%源~网[答案]　D

18．(14分)已知函数f(x)＝ax²+(2a－1)x－3在区间上的最大值为1，求实数a的值．

[解析]　当a＝0时，f(x)＝－x－3，

f(x)在上不能取得1，故a≠0.

∴f(x)＝ax²+(2a－1)x－3(a≠0)的对称轴方程为x₀＝.

(1)令f＝1，解得a＝－，

此时x₀＝－∈，

因为a<0，f(x₀)最大，所以f＝1不合适；

(2)令f(2)＝1，解得a＝，

此时x₀＝－∈，

因为a＝>0，x₀＝－∈，且距右端点2较远，所以f(2)最大，合适；

(3)令f(x₀)＝1，得a＝(－3±2)，

验证后知只有a＝(－3－2)才合适．

综上所述，a＝，或a＝－(3+2)．