
题目列表(包括答案和解析)
17.如图(1),在三角形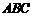 中,
中,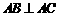 ,若
,若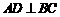 ,则
,则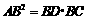 ;若类比该命题,如图(2),三棱锥
;若类比该命题,如图(2),三棱锥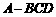 中,
中,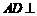 面
面
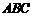 ,若
,若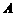 点在三角形
点在三角形 所在平面内的射影为
所在平面内的射影为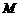 ,则有什么结论?命题是否是真命题.
,则有什么结论?命题是否是真命题.
解:命题是:三棱锥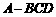 中,
中,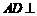 面
面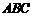 ,若
,若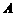 点在三角形
点在三角形 所在平面内的射影为
所在平面内的射影为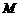 ,则有
,则有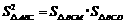 是一个真命题.
是一个真命题.
证明如下:
在图(2)中,连结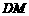
 ,并延
,并延 长交
长交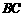 于
于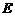 ,连结
,连结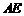 ,则有
,则有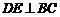 .
.
因为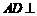 面
面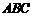 ,,所以
,,所以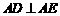 .
.
又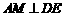 ,所以
,所以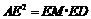 .
.
于是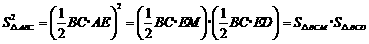 .
.
16.下面是按照一定规律画出的一列“树型”图:
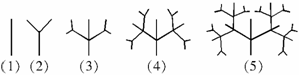
设第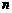 个图有
个图有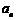 个树枝,则
个树枝,则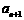 与
与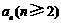 之间的关系是 .
之间的关系是 .
答案: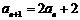
15.由三角形的性质通过类比推理,得到四面体的如下性质:四面体的六个二面角的平分面交于一点,且这个点是四面体内切球的球心,那么原来三角形的性质为 .
答案:三角形内角平分线交于一点,且这个点是三角形内切圆的圆心
14.已知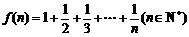 ,用数学归纳法证明
,用数学归纳法证明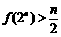 时,
时,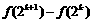 等于 .
等于 .
答案: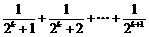
13.写出用三段论证明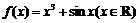 为奇函数的步骤是 .
为奇函数的步骤是 .
答案:满足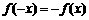 的函数是奇函数, 大前提
的函数是奇函数, 大前提
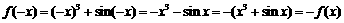 , 小前提
, 小前提
所以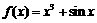 是奇函数. 结论
是奇函数. 结论
12.正整数按下表的规律排列
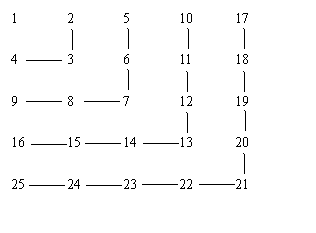
则上起第2005行,左起第2006列的数应为( )
A. B.
B. C.
C.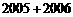 D.
D.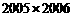
答案:D
11.类比“两角和与差的正余弦公 式”的形式,对于给定的两个函数,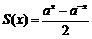 ,
,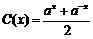 ,其中
,其中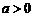 ,且
,且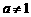 ,下面正确的运算公式是( )
,下面正确的运算公式是( )
①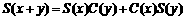 ;
;
②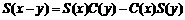 ;
;
③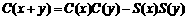 ;
;
④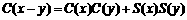 ;
;
A.①③ B.②④ C.①④ D.①②③④
答案:D
10.用数学归纳法证明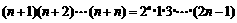 ,从
,从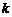 到
到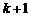 ,左边需要增乘的代数式为( )
,左边需要增乘的代数式为( )
A.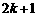 B.
B.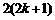 C.
C.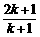 D.
D.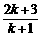
答案:B
9.用反证法证明命题:若整系数一元二次方程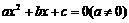 有有理根,那么
有有理根,那么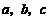 中至少有一个是偶数时,下列假设中正确的是( )
中至少有一个是偶数时,下列假设中正确的是( )
A.假设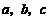 都是偶数
都是偶数
B.假设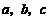 都不是偶数
都不是偶数
C.假设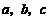 至多有一个是偶数
至多有一个是偶数
D.假设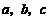 至多有两个是偶数
至多有两个是偶数
答案:B
8.已知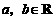 ,且
,且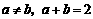 ,则( )
,则( )
A.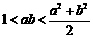 B.
B.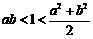
C.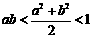 D.
D.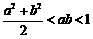
答案:B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com