16．(12分)设函数f(x)＝ax²+(b－8)x－a－ab的两个零点分别是－3和2；

(1)求f(x)；

(2)当函数f(x)的定义域是[0,1]时，求函数f(x)的值域．

[解析]　(1)∵f(x)的两个零点是－3和2，

∴函数图象过点(－3,0)、(2,0)，

∴有9a－3(b－8)－a－ab＝0，①

4a+2(b－8)－a－ab＝0.②

①－②得b＝a+8.③

③代入②得4a+2a－a－a(a+8)＝0，即a²+3a＝0.

∵a≠0，a＝－3，∴b＝a+8＝5.

∴f(x)＝－3x²－3x+18.

(2)由(1)得f(x)＝－3x²－3x+18＝－3(x+)²++18，图象的对称轴方程是x＝－，又0≤x≤1，

∴f(x)_min＝f(1)＝12，f(x)_max＝f(0)＝18，

∴函数f(x)的值域是[12,18]．

15．(12分)若函数y＝ax²－x－1只有一个零点，求实数a的取值范围．

[解析]　(1)若a＝0，则f(x)＝－x－1为一次函数，函数必有一个零点－1.

(2)若a≠0，函数是二次函数，因为二次方程ax²－x－1＝0只有一个实数根，所以Δ＝1+4a＝0，得a＝－.

综上，当a＝0和－时函数只有一个零点．

14．函数y＝x²与函数y＝2ln x在区间(0，+∞)上增长较快的是________．

[答案]　y＝x²

13．将进货单价为80元的商品按90元一个售出时，能卖出400个，已知该商品每个涨价1元，其销售量就减少20个，为了赚得最大利润，售价应定为________元．

[解析]　设该商品每个涨价x元时，利润为y元，则y＝(10+x)(400－20x)＝－20(x－5)²+4 500,0≤x<20.

当x＝5时，y取最大值4 500.

[答案]　95

12．已知函数y＝f(x)是R上的奇函数，其零点为x₁，x₂，…，x_{2 009}，则x₁+x₂+…+x_{2 009}＝________.

[解析]　定义在R上的奇函数f(x)必有f(0)＝0，则x₁，x₂，…，x_{2 009}中必有一个是0，其余的2 008个零点分别在x轴上，关于坐标原点两两对称．

[答案]　0

11．函数f(x)＝(x²－2)(x²－3x+2)的零点为________．

[解析]　由f(x)＝(x²－2)(x²－3x+2)＝0得

x＝±或x＝1或x＝2.

∴函数f(x)的零点为－，1，，2.

[答案]　－，1，，2

10.

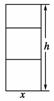
利用一根长6米的木料，做一个如图的矩形窗框(包括中间两条横档)，则窗框的高和宽的比值为多少时透过的光线最多(即矩形窗框围成的面积最大)(　)

A．1.5　 B．2

C．0.5　 D．1

[解析]　设窗框的宽为x，高为h，

则2h+4x＝6，

即h+2x＝3，∴h＝3－2x，

∴矩形窗框围成的面积

S＝x(3－2x)

＝－2x²+3x(0<x<)，

当x＝－＝＝0.75时，

S有最大值．

∴h＝3－2x＝1.5，

∴高与宽之比为2.故选B.

[答案]　B

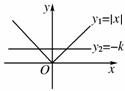
9．函数f(x)＝|x|－k有两个零点，则(　)

A．k<0　 B．k>0

C．0≤k<1　 D．k＝0

[解析]　在同一坐标系中画出y₁＝|x|和y₂＝－k，若f(x)有两个零点，必有－k>0，即k<0.故选A.

[答案]　A

8．某城市为保护环境，维护水资源，鼓励职工节约用水，作出了如下规定：每月用水不超过8吨，按每吨2元收取水费；每月超过8吨，超过部分加倍收费，某职工某月缴费20元，则该职工这个月实际用水(　)

A．10吨　 B．13吨

C．11吨　 D．9吨

[解析]　设该职工该月实际用水为x吨，易知x>8.

则水费y＝16+2×2(x－8)

＝4x－16＝20，

∴x＝9.故选D.

[答案]　D

7．某宾馆共有客床100张，各床每晚收费10元时可全部住满，若每晚收费每提高2元，便减少10张客床租出，则总收入y(y>0)元与每床每晚收费应提高x(假设x是2的正整数倍)元的关系式为(　)

A．y＝(10+x)(100－5x)

B．y＝(10+x)(100－5x)，x∈N

C．y＝(10+x)(100－5x)，x＝2,4,6,8，…，18

D．y＝(10+x)(100－5x)，x＝2,4,6,8

[解析]　由题可得总收入y与x之间的函数关系式为：y＝(10+x)(100－5x)，x＝2,4,6,8，…，18.故选C.

[答案]　C