
题目列表(包括答案和解析)
(三)解答题
16、空间四边形ABCD中,E、F分别是AB和CB的中点,G、H分别是CD和AD上的点,且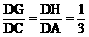 ,求证:EF、FG、BD三条直线交于一点。
,求证:EF、FG、BD三条直线交于一点。
17、正方体ABCD-A1B1C1D1的棱长为a,M、N分别是AA1、D1C1的中点,过D、M、N三点的平面与正方体的下底面相交于直线l。
(1)画出直线l;(2)设l∩A1B1=P,求线段PB1的长。
18、画出满足条件的图形:
α∩β=l,AB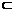 α,CD
α,CD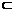 β,AB∥l,CD∥l。
β,AB∥l,CD∥l。
19、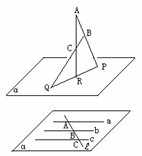 如图,△ABC在平面α外,AB∩α=P,BC∩α=Q,AC∩α=R,求证:P、Q、R三点共线。
如图,△ABC在平面α外,AB∩α=P,BC∩α=Q,AC∩α=R,求证:P、Q、R三点共线。
20、已知直线a∥b∥c,l∩a=A,l∩a=A,l∩b=B,l∩c=C,求证:a,b,c,l四线共面。
该命题可作怎样的推广?
第2讲空间的平行直线和异面直线
(二)填空题
8、不共面的四点可以确定________个平面。
9、一条直线过平面内一点与平面外一点,它和这个平面有________个公共点。
10、如图,平面ABC和平面DEF的交点有________个。
11、P为正方体ABCD-A1B1C1D1的棱B1C1上的点(异于B1、C1),则直线A1P必与棱______所在直线相交。
12、如图为水平放置的△ABC的直观图,由图判定原三角形中AB、BO、BD、OD由小到大的顺序__________。
13、空间三个平面的交线条数为k,则k的可能值是__________。
14、α∩β=BC,A∈α,D∈β,E、F、G、H分别是AB、AC、CD、DB上的点,若EF∩GH=P,则点P必在直线________上。
15、空间三条直线a,b,c互相平行,但不共面,它们能确定______个平面;这些平面把空间分成______个部分。
(一) 选择题
1、 空间四点中“三点共线”是“四点共面”的
A、充分不必要 B、必要不充分
C、充分且必要 D、既不充分也不必要
2、下面列举了四个关于空间中直线共面的条件:(1)三条直线两两相交;(2)三条直线两两平行;(3)三条直线共点;(4)三条直线有两条平行。其中不正确的个数是
A、 1个 B、2个 C、3个 D、4个
3、 直线a,b,c交于一点,经过这三条直线的平面
A、1个 B、3个 C、无数个 D、可以为0个,可以为1个
4、 三个平面最多可以把空间分成
A、 4个部分 B、6个部分 C、7个部分 D、8个部分
5、已知α∩β=l,M∈α,N∈α,P∈β,P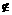 l,MN∩l=R,记过M、N、P三点的平面γ,则β∩γ等于
l,MN∩l=R,记过M、N、P三点的平面γ,则β∩γ等于
A、直线MP B、直线PR C、直线NP D、直线MR
6、空间四点A、B、C、D共面但不共线,则下面结论成立的是
A、四点中必有三点共线
B、四点中必有三点不共线
C、AB、BC、CD、DA四条直线中总有两条平行
D、AB与CD必相交
7、正方体ABCD-A1B1C1D1的棱长为4,过点A、B1、D1三点的平面与平面A1B1C1D1相交于直线l,则点A到直线l的距离为
A、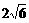 B、
B、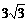 C、
C、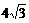 D、
D、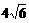
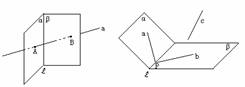 例1、用符号语言写出下列图形应满足的条件
例1、用符号语言写出下列图形应满足的条件
图(1) 图(2)
分析;根据图形,准确 地想象点、线、面这些基本元素的关系,然后用集合的符号语言表示出来。书写的规律一般是:先平面再直线,最后为点。
在(1)中:平面α∩平面β=l,a∩α=A,b∩α=B
在(2)中:α∩β=l,a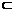 α,b
α,b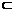 β,a∩l=P, b∩l=P,c∥l。
β,a∩l=P, b∩l=P,c∥l。
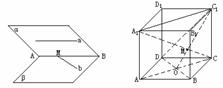 例2、作出满足下列条件的图形:
例2、作出满足下列条件的图形:
图(1) 图(2)
(1) α∩β=AB,a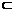 α,b
α,b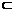 β,a∥AB,b∩AB=M;
β,a∥AB,b∩AB=M;
(2) 正方体ABCD-A1B1C1D1中,O为正方形ABCD中心,A1C∩平面C1BD=M,求作点M。
分析:(1)作图的顺序与读图的顺序相同,先平面再直线再到点。如图(1)
(2)设法把点M放到某两个平面的交线上,∵M∈A1C,A1C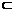 平面AA1C1C(由AA1∥C1C,A1A,CC1是可以确定一个平面的),∴M∈平面AA1C1C。又M∈平面C1BD,∴M为平面AA1C1C与平面C1BD的公共点。观察图象可知,C1、O也为上述两个平面的公共点,即平面AA1C1C∩平面C1BD=C1O。∵M∈C1O,又M∈A1C,∴C1O∩A1C=M,即平面AA1C1C1内,两直线C1O与A1C的公共点就是所求作的点M。
平面AA1C1C(由AA1∥C1C,A1A,CC1是可以确定一个平面的),∴M∈平面AA1C1C。又M∈平面C1BD,∴M为平面AA1C1C与平面C1BD的公共点。观察图象可知,C1、O也为上述两个平面的公共点,即平面AA1C1C∩平面C1BD=C1O。∵M∈C1O,又M∈A1C,∴C1O∩A1C=M,即平面AA1C1C1内,两直线C1O与A1C的公共点就是所求作的点M。
评注:题(2)首先体现了转化的思想,将在空间难以把握的线面交点转化为同一平面内的线线交点,确定了交点的位置。其次,将直线A1C放在平面AA1C1C内思考,这是处理直线典型的一种思考方法。借助于平面AA1C1C,点M的位置就越来越具体了。这种类似于平面几何辅助直线的平面,称之为辅助平面。在研究空间图形时,经常要作这样的辅助平面。进一步研究M点性质,还可发现M为A1C的三等分点,M是△C1BD的重心(中心)。
例3、求证:两两相交且不过同一点的四条直线共面。
分析:以文字语言出现的几何证明题,首先要“翻译”为符号语言写成已知、求证的形式,并辅之以正确的图形,然后再进行证明。
已知:四条直线a,b,c,d两两相交,不过同一点。
求证:a,b,c,d共面。
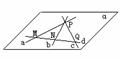 在正确分析四条直线位置关系时,可利用逐步添加的方法。当在两条直线上添加第三条直线时,可以发现存在下列两种位置关系;三线共点和三线不共点。因此本题需分两种情况证明:
在正确分析四条直线位置关系时,可利用逐步添加的方法。当在两条直线上添加第三条直线时,可以发现存在下列两种位置关系;三线共点和三线不共点。因此本题需分两种情况证明:
(1) 当存在三线共点时,如右图:
设a,b,c共点于Q,d∩a=M,d∩b=N,d∩c=Q
∵ a∩b=P
∴ a,b可确定平面α
∵ M∈a,N∈b
∴ M∈α,N∈α
∵ M∈d,N∈d
∴ d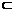 α
α
∴ Q∈α
又P∈c,Q∈c
∴ c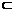 α
α
∴ a,b,c,d共面于α。
(2) 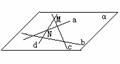 任何三条直线都不共点时
任何三条直线都不共点时
∵ a,b,c,d两两不相交且不过同一点
∴ a,b,c,d可确定平面α
设d∩a=N,d∩b=M
则M∈α,N∈α
又N∈d,M∈d
∴ d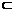 α
α
∴ a,b,c,d共面于α。
评注:在证明几何问题,一忌用直观代替严谨的逻辑证明,如直接看图得出结论。因为直观图仅仅是直观,是对空间真实位置关系的某种“歪曲”反映,看到的不一定就是实际真实位置;二忌跳步,在结论之前缺乏有序有步骤有层次的推导。三忌程序混乱,不知道应该先说什么,再说什么。当然,还有符号、语言的准确性等等。
4. 方程|x|+|y-1|=2所表示的直线而构成的图形的面积为_____________
3.已知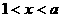 ,则
,则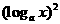 与
与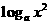 的大小关系是
的大小关系是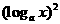
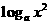 。
。
2. 点(1,cosθ)到直线xsinθ+ycosθ=1的距离是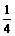 (0≤θ≤π),则θ=_______
(0≤θ≤π),则θ=_______
1. 已知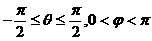 则
则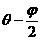 的范围
。
的范围
。
(1)下列说法不正确的是( )若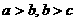 则
则
A.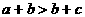 B.
B.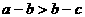
C.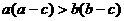 D.
D.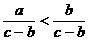
(2)下列说法中正确的有( )个
A.1个 B.2个 C.3个 D.4个
Ⅰ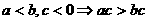 Ⅱ
Ⅱ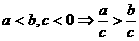
Ⅲ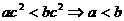 Ⅳ
Ⅳ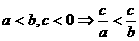
(3)直线kx-y+1=3k,当k变动时,所有直线都通过定点( )
(A)(0,0) (B)(0,1) (C)(3,1) (D)(2,1)
(4)直线l1:x-y+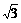 -1=0绕着它上面一点(1,
-1=0绕着它上面一点(1,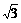 )沿逆时针方向旋转15°,则旋转后的直线l2的方程为( )
)沿逆时针方向旋转15°,则旋转后的直线l2的方程为( )
(A)x-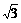 y+1=0 (B)3x-
y+1=0 (B)3x-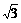 y=0 (C)
y=0 (C)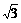 x+y+1=0 (D)3x-
x+y+1=0 (D)3x-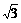 y-1=0
y-1=0
(5)如果AC<0且BC<0,那么直线Ax+By+C=0不通过( )
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
(6)直线2x+3y-6=0关于直线x=0对称的直线方程为( )
(A) 2x-3y-6=0 (B)2x-3y+6=0 (C)2x+3y+6=0 (D)2x+3y-6=0
(7)给出平面区域如图所示,若使目标函数z=ax+y (a>0)取得最大值的最优解有无穷个,则a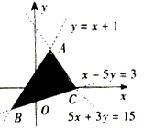 的值为( ).
A、
的值为( ).
A、 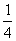 B、
B、 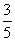 C、4 D、
C、4 D、 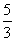
(8)不等式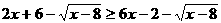 的解是
的解是
A.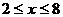 B.
B.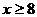
C.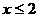 D.以上都不对
D.以上都不对
(9)直线(2m2+m-2)x+(m2-m)y+4m-1=0与直线2x-3y=5平行,则m=( )
(A)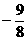 (B)2 (C)2或
(B)2 (C)2或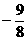 (D)1或
(D)1或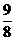
(10) 已知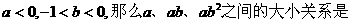
A.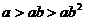 B.
B.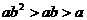
C.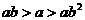 D.
D.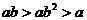
(11)如果直线经过两直线2x-3y+1=0和3x-y-2=0的交点,且与直线y=x垂直,则原点到直线l的距离是( )
(A)2
(B)1
(C)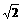 (D)2
(D)2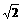
(12)已知两点A(1,3),B(-1-5),在直线2x+3y+1=0上有一点P,使|PA|=|PB|,则P点的坐标是( )
(A)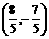 (B)
(B)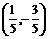 (C)(2,-1) (D)(5,0)
(C)(2,-1) (D)(5,0)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com