
题目列表(包括答案和解析)
4.点P的曲线y=x3-x+上移动,在点P处的切线的倾斜角为α,则α的取值范围 .
3.曲线y= x3-x2+5在x=1处的切线的倾斜角是 .
2.已知函数f(x)=(2x+a)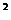 ;若f(x)在x=a处的导数值为20,则 a=
.
;若f(x)在x=a处的导数值为20,则 a=
.
1.设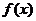 在
在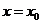 处可导,且
处可导,且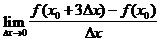 =1,则
=1,则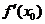 =( )
=( )
A.1
B.0 C.3 D.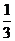
20.已知下表给出的是由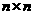 (
(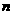 ≥3,
≥3,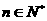 )个正数排成的
)个正数排成的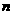 行
行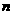 列数表,
列数表,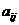 表示第
表示第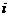 行第
行第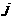 列的一个数,表中第一列的数从上到下依次成等差数列,其公差为
列的一个数,表中第一列的数从上到下依次成等差数列,其公差为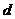 ,表中各行,每一行的数从左到右依次都成等比数列,且所有公比为
,表中各行,每一行的数从左到右依次都成等比数列,且所有公比为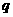 ,已知
,已知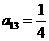 ,
,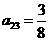 ,
,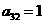 。
。
(Ⅰ)求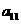 ,
,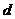 ,
,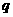 的值;
的值;
(Ⅱ)设表中对角线的数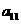 ,
,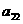 ,
,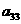 ,
, ,
, 组成的数列为
组成的数列为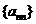 ,记
,记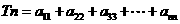 ,求使不等式
,求使不等式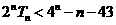
成立的最小正整数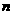 。
。
19.已知函数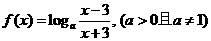 。
。
(Ⅰ)判定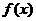 在
在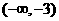 上的单调性,并证明;
上的单调性,并证明;
(Ⅱ)设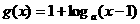 ,若方程
,若方程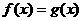 有实根,求
有实根,求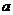 的取值范围.
的取值范围.
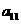
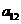
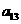



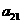
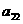
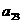
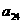

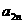
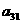
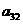
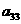
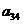

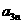






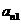
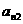
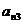
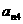


18.已知B2,B1分别是中心在原点、焦点在x轴上的椭圆C的上、下顶点,F是C的右焦点,FB1=2,F到C的左准线的距离是.
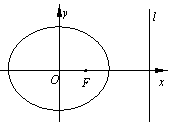 (1)求椭圆C的方程;
(1)求椭圆C的方程;
(2)点P是C上与B1,B2不重合的动点,直线B1P,
B2P与x轴分别交于点M,N.求证: 是定值.
17.某纺纱厂生产甲、乙两种棉纱,已知生产甲种棉纱1吨需耗一级子棉2吨,二级子棉1吨;生产乙种棉纱1吨需耗一级子棉1吨,二级子棉2吨;每一吨甲种棉纱的利润是600元,每一吨乙种棉纱的利润是900元,工厂在生产这两种棉纱的计划中要求消耗一级子棉不超过300吨、二级子棉不超过250吨。甲、乙两种棉纱应各生产多少吨,才能能使利润总额最大?
16.如图,四棱锥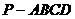 中,底面
中,底面 是边长为2的正方形,
是边长为2的正方形, ,且
,且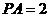 ,
,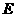 为
为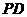 中点.
中点.
(Ⅰ)求证: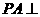 平面
平面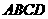 ;
;
(Ⅱ)求二面角 的余弦值;
的余弦值;
 (Ⅲ)在线段
(Ⅲ)在线段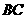 上是否存在点
上是否存在点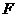 ,使得点
,使得点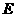 到平面
到平面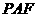 的距离为
的距离为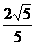 ?若存在,确定点
?若存在,确定点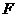 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
15.已知a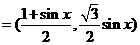 ,b
,b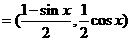 ,
,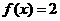 a·b+1.
(I)求函数
a·b+1.
(I)求函数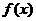 的最小正周期和最大值;
(II)该函数的图象可由
的最小正周期和最大值;
(II)该函数的图象可由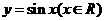 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com