
题目列表(包括答案和解析)
6.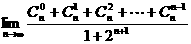 的值为( )
的值为( )
(A)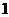 (B)
(B)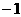 (C)
(C) (D)
(D)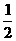
5.将编号为1,2,3,4,5,6的六个小球排成一列,要求1号球与2号球必须相邻,5号球与6号球不相邻,则不同的排法种数有( )
(A)36 (B)142 (C)48 (D)144
4.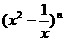 的展开式中,常数项为15,则
的展开式中,常数项为15,则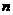 等于( )
等于( )
(A)3 (B)4 (C)5 (D)6
3.3名男生2名女生排成一排,女生甲始终排在女生乙的左边的排法种数是( )
(A)120 (B)60 (C)48 (D)24
2.要从四个学校中选出6人作“市优干”,每校至少一名,这6个名额有( )种分配方法.
(A)15 (B)20 (C)10 (D)6
1.某研究所有编号为1,2,3,4的四个饲养房,分别饲养有18、54、24、48只白鼠供试验用,某项试验需抽取24只白鼠,你认为最合适的抽样方法为( )
(A)在每个饲养房各抽取6只
(B)为所有白鼠都加上编有不同号码的项圈,用随机抽样法确定24只
(C)在四个饲养房分别抽取3、9、4、8只
(D)先确定这四个饲养房应分别抽出3、9、4、8只样品,再由各饲养房自己加号码项圈,用简单随机抽样确定各自抽出的对象
20、已知数列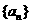 满足
满足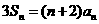 ,其中
,其中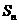 为其前
为其前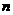 项的和,
项的和,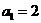 。
。
(1)证明:数列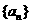 的通项公式为
的通项公式为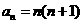 ;
;
(2)求数列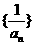 的前
的前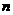 项和
项和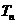 ;
;
(3)是否存在无限集合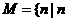 为正整数}, 总有
为正整数}, 总有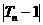 <
<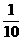 成立;若存在,请找出一个这样的集合;若不存在,请说明理由。
成立;若存在,请找出一个这样的集合;若不存在,请说明理由。
证明(1)当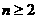 时,
时,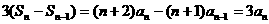 ,
,
整理得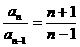 。
。
于是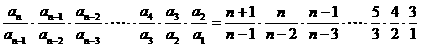 ,
,
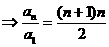
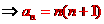 。
。
(2)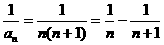 ,
,
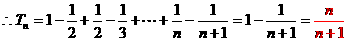 。
。
(3)要使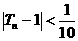 ,即
,即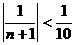 ,只需
,只需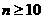 即可。
即可。
所以, 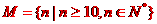 。
。
19、已知数列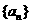 满足
满足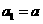 (
(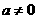 ,且
,且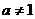 ),其前
),其前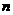 项和
项和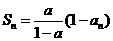 。
。
(1)求证: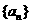 为等比数列;
为等比数列;
(2)记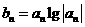 (
(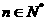 ),
),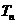 为数列
为数列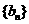 的前
的前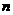 项和。当
项和。当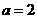 时,求
时,求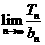 。
。
证明:(1)当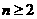 时,
时,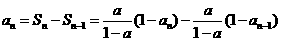 ,
,
整理得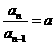 ,
,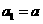 ,所以
,所以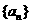 是以
是以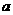 为首项,
为首项,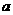 为公比的等比数列。
为公比的等比数列。
于是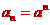 。
。
(2)因为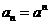 ,
,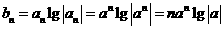 。
。
当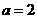 时,
时,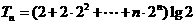 ,
,
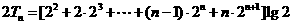 ,
,
两式相减得,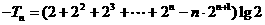
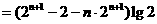
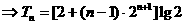 ,又
,又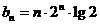 ,
,
所以,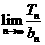
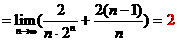 。
。
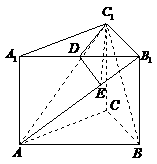
18、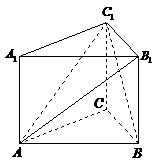 直三棱柱
直三棱柱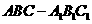 中,
中,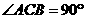 ,
,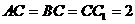 。
。
(1)证明: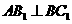 ;
;
(2)求点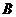 到平面
到平面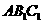 的距离;
的距离;
(3)求二面角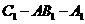 的大小。
的大小。
解:(1)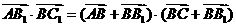
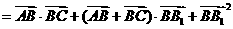
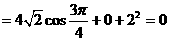 ,
,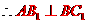 。
。
(2)设点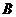 到平面
到平面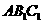 的距离为
的距离为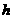 ,
,
因为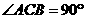 ,
,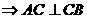 ,又
,又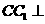 平面
平面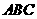 ,则
,则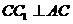 ,
,
 平面
平面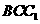 。
。
同理得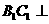 平面
平面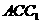 ,所以
,所以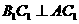 。
。
于是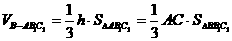 。
。
因为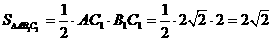 ,
,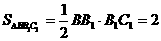 ,
,
所以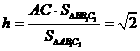 。
。
 故点
故点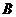 到平面
到平面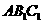 的距离为
的距离为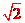 。
。
(3)取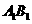 中点
中点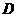 ,联结
,联结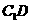 ,过
,过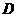 作
作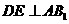 交于
交于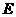 ,联结
,联结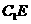 。
。
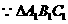 是等腰三角形,
是等腰三角形,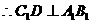 。
。
又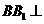 平面
平面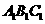 ,
,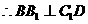 ,所以
,所以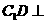 平面
平面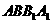 。
。
于是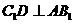 ,又
,又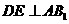 ,
,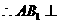 平面
平面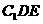 ,得
,得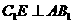 。
。
因此,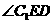 为二面角
为二面角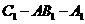 的平面角。
的平面角。
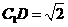 ,
,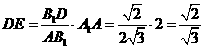 ,
,
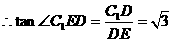 ,即
,即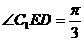 。
。
所以二面角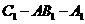 的大小为
的大小为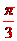 。
。
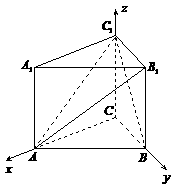 另解:(空间向量)
另解:(空间向量)
(1)建立空间直角坐标系如图,则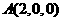 ,
,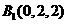 ,
,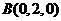 ,
,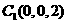 。
。
于是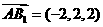 ,
,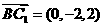 。
。
则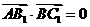 ,所以
,所以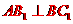 。
。
(2)设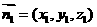 是平面
是平面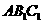 的法向量,
的法向量,
由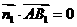 ,
,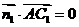 ,得
,得
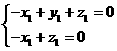 ,所以
,所以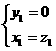 。
。
令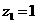 ,则
,则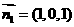 。
。
又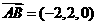 ,所以
,所以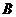 到平面
到平面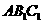 的距离
的距离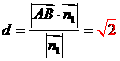 。
。
(3)设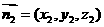 是平面
是平面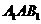 的法向量,
的法向量,
由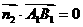 ,
,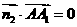 得
得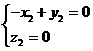 ,所以
,所以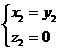 。
。
令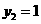 ,则
,则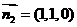 。
。
因为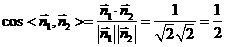 ,
,
所以,二面角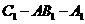 的平面角的大小为
的平面角的大小为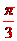 。
。
17、如图,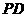 垂直正方形
垂直正方形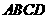 所在平面,
所在平面,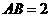 ,
,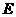 是
是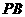 的中点,向量
的中点,向量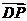 、
、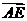 的夹角为
的夹角为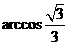 。
。
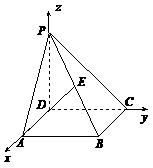 (1)建立适当的坐标系,求点
(1)建立适当的坐标系,求点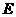 的坐标;
的坐标;
(2)在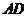 上找一点
上找一点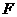 ,使
,使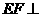 平面
平面 。
。
解:(1)以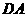 、
、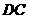 、
、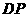 所在的直线分别为
所在的直线分别为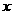 轴、
轴、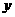 轴、
轴、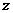 轴建立空间直角坐标系如图,则
轴建立空间直角坐标系如图,则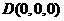 ,
,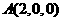 。设
。设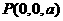 (
(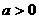 ),
),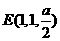 。
。
于是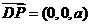 ,
,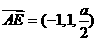 。
。
由题意得,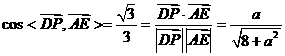 ,
,
解得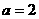 或
或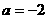 (舍)。
(舍)。
所以点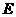 的坐标为
的坐标为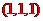 。
。
(2)设点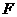 的坐标为
的坐标为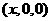 ,则
,则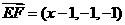 。
。
要使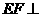 平面
平面
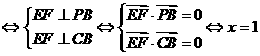 。
。
所以点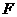 的坐标为
的坐标为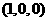 ,即点
,即点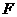 为
为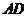 的中点。
的中点。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com