
题目列表(包括答案和解析)
9、已知△ABC中,sinA∶sinB∶sinC=k∶(k+1)∶2k (k≠0),则k的取值范围为( )
A.(2,+∞) B.(-∞,0) C.(-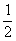 ,0) D.(
,0) D.(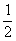 ,+∞)
,+∞)
8、已知¦(n)= 1+ + + +…+ 则¦(n+1)- ¦(n)之值为( )
A B C + D + +
7、⊿ABC为钝角三角形,a=3,b=4,c=x,C为钝角,则x的取值范围为( )
A 5<x<7 B x<5 C 1<x<5 D 1<x<7
6、某种细菌在培养过程中,每20分钟分裂一次(一个分裂二个)经过3小时,这种细菌由1个可以繁殖成( )A.511个 B.512个 C.1023个 D.1024个
5、若数列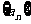 中,
中,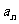 = 43-3n,则
= 43-3n,则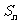 最大值n=
( )
最大值n=
( )
A.13 B.14 C.15 D.14或15
4、设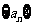 是公差为正数的等差数列,若
是公差为正数的等差数列,若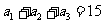 ,
,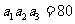 ,则
,则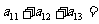 ( ) A.
( ) A.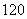 B.
B.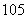 C.
C.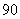 D.
D.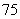
3、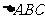 的三角A、B、C所对的边a、b、c成等比数列,则∠B的取值范围是( )
的三角A、B、C所对的边a、b、c成等比数列,则∠B的取值范围是( )
A.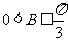 B.
B.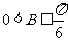 C.
C.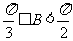 D.
D.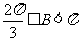
2、已知△ABC中,a=4,b=4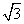 ,∠A=30°,则∠B等于( )
,∠A=30°,则∠B等于( )
A.30° B.30°或150° C.60° D.60°或120°
1、若lga、lgb、lgc成等差数列,则有( )
A、b=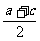 B、b=
B、b=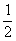 (lga+lgc) C、 a、b、c成等比数列 D、a、b、c成等差数列
(lga+lgc) C、 a、b、c成等比数列 D、a、b、c成等差数列
22.(本小题满分14分)
已知函数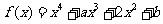 (
(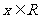 ),其中
),其中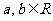 .
.
(Ⅰ)当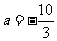 时,讨论函数
时,讨论函数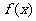 的单调性;
的单调性;
(Ⅱ)若函数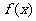 仅在
仅在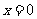 处有极值,求
处有极值,求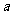 的取值范围;
的取值范围;
(Ⅲ)若对于任意的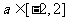 ,不等式
,不等式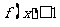 在
在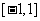 上恒成立,求
上恒成立,求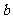 的取值范围.
的取值范围.
本小题主要考查利用导数研究函数的单调性、函数的最大值、解不等式等基础知识,考查综合分析和解决问题的能力.满分14分.
(Ⅰ)解: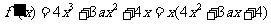 .
.
当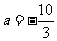 时,
时,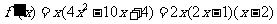 .
.
令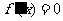 ,解得
,解得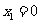 ,
,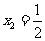 ,
,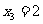 .
.
当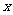 变化时,
变化时,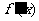 ,
,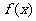 的变化情况如下表:
的变化情况如下表:
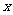 |
 |
0 |
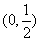 |
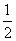 |
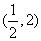 |
2 |
 |
 |
- |
0 |
+ |
0 |
- |
0 |
+ |
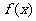 |
↘ |
极小值 |
↗ |
极大值 |
↘ |
极小值 |
↗ |
所以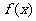 在
在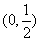 ,
, 内是增函数,在
内是增函数,在 ,
,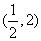 内是减函数.
内是减函数.
(Ⅱ)解: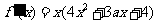 ,显然
,显然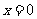 不是方程
不是方程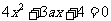 的根.
的根.
为使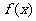 仅在
仅在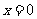 处有极值,必须
处有极值,必须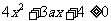 成立,即有
成立,即有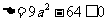 .
.
解些不等式,得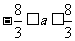 .这时,
.这时,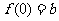 是唯一极值.
是唯一极值.
因此满足条件的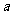 的取值范围是
的取值范围是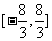 .
.
(Ⅲ)解:由条件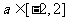 ,可知
,可知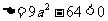 ,从而
,从而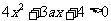 恒成立.
恒成立.
当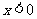 时,
时,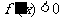 ;当
;当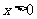 时,
时,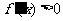 .
.
因此函数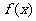 在
在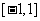 上的最大值是
上的最大值是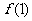 与
与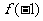 两者中的较大者.
两者中的较大者.
为使对任意的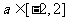 ,不等式
,不等式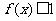 在
在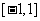 上恒成立,当且仅当
上恒成立,当且仅当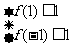 ,即
,即 ,在
,在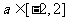 上恒成立.
上恒成立.
所以 ,因此满足条件的
,因此满足条件的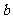 的取值范围是
的取值范围是 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com