
7.如图,已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是
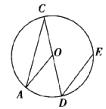
A.25° B.40° C.30° D.50°
6.如图,箭头表示投影的方向,则图中圆柱体的投影是
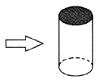
A.圆 B.矩形 C.梯形 D.圆柱
5.下列成语所描述的事件是必然事件的是
A.瓮中捉鳖 B.拔苗助长 C.守株待兔 D.水中捞月
4.五箱苹果的质量分别为(单位:千克):18,20,21,22,19,则这五箱苹果质量的平均数和中位数分别为
A.19和20 B.20和19 C.20和20 D.20和21
3.新建的北京奥运会体育场--“鸟巢”能容纳91 000位观众,将91 000用科学记数法表示为
A.91×103 B.910×102 C.9.1×104 D.9.1×103
2.下列计算正确的是
A.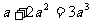 B.
B.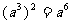 C.
C.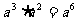 D.
D.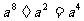
1.3的相反数是
A.3 B.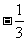 C.
C.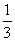 D.-3
D.-3
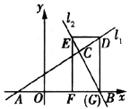
26.(本题l4分)如图,已知直线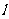 1:
1: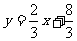 与直线
与直线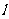 2:
2: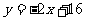 相交于点C,
相交于点C,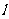 1、
1、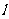 2分别交
2分别交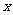 轴于A、B两点,矩形DEFG的顶点D、E分别在直线
轴于A、B两点,矩形DEFG的顶点D、E分别在直线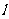 1、
1、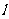 2上,顶点F、G都在
2上,顶点F、G都在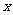 轴上,且点G与点B重合.
轴上,且点G与点B重合.
(1)求△ABC的面积;
(2)求矩形DEFG的边DE与EF的长;
(3)若矩形DEFG从原地出发,沿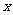 轴的反方向以每秒1个单位长度的速度平移,设移动时间为t(0≤t≤12)秒,矩形DEFG与△ABC重叠部分的面积为S,求S关于t的函数关系式,并写出相应的t的取值范围.
轴的反方向以每秒1个单位长度的速度平移,设移动时间为t(0≤t≤12)秒,矩形DEFG与△ABC重叠部分的面积为S,求S关于t的函数关系式,并写出相应的t的取值范围.
25.(本题l2分)在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B顺时针旋转角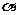 (0°<
(0°<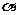 <90°)得△AlBCl,AlB交AC于点E,A1C1分别交AC、BC于D、F两点.
<90°)得△AlBCl,AlB交AC于点E,A1C1分别交AC、BC于D、F两点.
(1)如图(1),观察并猜想,在旋转过程中,线段EA1与FC有怎样的数量关系?并证明你的结论;
(2)如图(2),当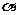 =30°时,试判断四边形BC1DA的形状,并说明理由;
=30°时,试判断四边形BC1DA的形状,并说明理由;
(3)在(2)的情况下,求ED的长.
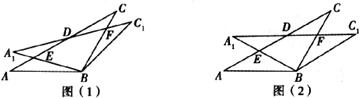
24.(本题8分)某批发市场批发甲、乙两种水果,根据以往经验和市场行情,预计夏季某一时间内,甲种水果的销售利润y甲(万元)与进货量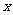 (吨)近似满足函数关系:y甲=0.3
(吨)近似满足函数关系:y甲=0.3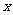 ;乙种水果的销售利润y乙(万元)与进货量
;乙种水果的销售利润y乙(万元)与进货量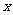 (吨)近似满足函数关系:y乙=
(吨)近似满足函数关系:y乙=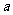
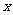 2+b
2+b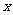 (其中
(其中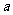 ≠0,
≠0,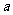 、b为常数),且进货量
、b为常数),且进货量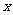 为1吨时,销售利润y乙为l.4万元;进货量
为1吨时,销售利润y乙为l.4万元;进货量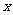 为2吨时,销售利润y乙为2.6万元.
为2吨时,销售利润y乙为2.6万元.
(1)求y乙(万元)与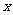 (吨)之间的函数关系式;
(吨)之间的函数关系式;
(2)如果市场准备进甲、乙两种水果共10吨,设乙种水果的进货量为t吨,请你写出这两种水果所获得的销售利润之和W(万元)与t(吨)之间的函数关系式,并求出这两种水果各进多少吨时获得的销售利润之和最大,最大利润是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com