
20.(本小题满分12分)
已知数列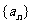 是首项a1=1的等比数列,其公比q是方程
是首项a1=1的等比数列,其公比q是方程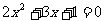 的根。
的根。
(I)求数列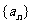 的通项公式和前n项和Sn;
的通项公式和前n项和Sn;
(II)当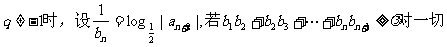
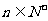 恒成立,求实数
恒成立,求实数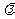 的取值范围。
的取值范围。
19.(本小题满分12分)
如图,在四棱锥P-ABCD中,ABCD是矩形。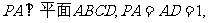
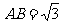 ,点F是PD的中点,点E在CD上移动。
,点F是PD的中点,点E在CD上移动。
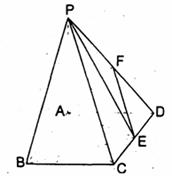
(I)求三棱锥E-PAB的体积;
(II)当点E为CD的中点时,试判断EF与平面PAC的关系,并说明理由;
(III)求证: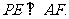
18.(本小题满分12分)
从某校高三年级共800名男生中随机抽取50名测量身高,据测量被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组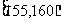 ,第二组
,第二组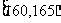 ,…第八组
,…第八组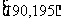 ,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人。
,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人。
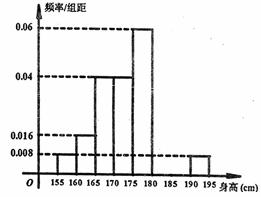
(I)估计这所学校高三年级全体男生身高180cm以上(含180cm)的人数;
(II)求第六组、第七组的频率;
(III)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为x,y,求满足: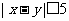 的事件概率。
的事件概率。
17.(本小题满分12分)
设函数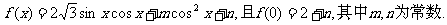
(I)求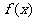 的单调递减区间;
的单调递减区间;
(II)若当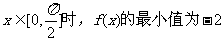 ,求n的值。
,求n的值。
16.对于一个有限数列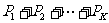 ,记为P,定义P的“蔡查罗和”为
,记为P,定义P的“蔡查罗和”为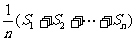 ,其PSk=
。
,其PSk=
。
15.已知 ,若目标函数
,若目标函数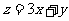 的最小值是5,则c=
。
的最小值是5,则c=
。
14.已知定义在R上的函数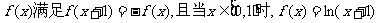 由
由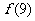 =
。
=
。
13.数列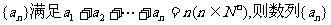 的通项为an=
。
的通项为an=
。
12.考察下列函数:
①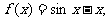 ②
②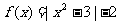
③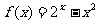 ④
④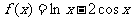
其中有三个零点的函数是 ( )
A.①② B.②③ C.③④ D.①④
第Ⅱ卷(非选择题,共90分)
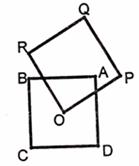
11.如图,两个边长都为2的正方形ABCD和OPQR,如果点O正好是正方形ABCD的中心,而正方形OPQR可以绕点O旋转。若向正方形ABCD内随机投郑一个质点,则它落在这两个正方形重叠部分的概率是 ( )
A.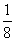 B.
B.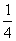 C.
C.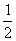 D.
D.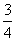
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com