
8.抽气机每次抽出容器内空气的60%,要使容器内剩下的空气少于原来的0.1%,则至少要抽(参考数据: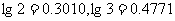 ) ( )
) ( )
A.15次 B.14次 C.9次 D.8次
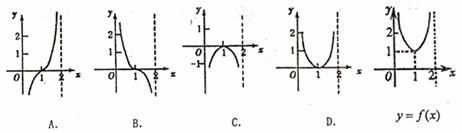
7.函数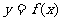 的图象如图所示,则函数
的图象如图所示,则函数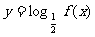 的图象大致是 ( )
的图象大致是 ( )
6.已知等差数列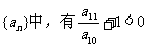 ,且它们的前n项和Sn有最大值,则使得
,且它们的前n项和Sn有最大值,则使得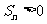 的n的最大值是 ( )
的n的最大值是 ( )
A.11 B.19 C.20 D.21
5.已知直线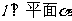 ,直线
,直线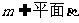 ,给出下列命题:
,给出下列命题:
①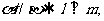 ②
②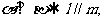
③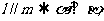 ④
④
其中正确的命题是 ( )
A.①②③ B.②③④ C.②④ D.①③
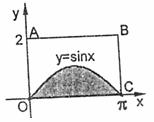
4.如下图,在一个长为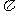 ,宽为2的矩形OABC内,曲线
,宽为2的矩形OABC内,曲线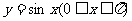 与x轴围成如图所示的阴影部分,向矩形OABC内随机投一点(该点落在矩形OABC内任何一点是等可能的),则所投的点落在阴影部分的概率是 ( )
与x轴围成如图所示的阴影部分,向矩形OABC内随机投一点(该点落在矩形OABC内任何一点是等可能的),则所投的点落在阴影部分的概率是 ( )
A.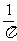 B.
B.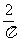 C.
C.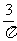 D.
D.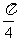
3.一个算法的程序框如图所示,若该程序输出的结果为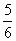 ,则判断框中应填入的条件是 ( )
,则判断框中应填入的条件是 ( )
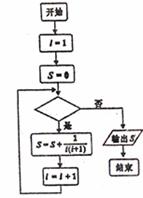
A.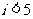 B.
B.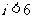
C.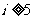 D.
D.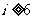
2.已知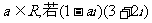 为纯虚数,则a的值为 ( )
为纯虚数,则a的值为 ( )
A.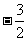 B.
B.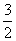 C.
C.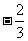 D.
D.
1.设集合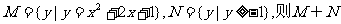 等于 ( )
等于 ( )
A.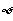 B.{(1,4)}
B.{(1,4)}
C.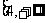 D.
D.
22.(本小题满分14分)
已知函数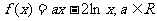
(I)求函数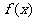 的极值;
的极值;
(II)对于曲线上的不同两点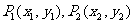 ,如果存在曲线上的点Q(
,如果存在曲线上的点Q(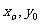 ),且
),且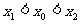 ,使得曲线在点Q处的切线
,使得曲线在点Q处的切线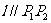 ,则称
,则称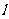 为弦P1P2的伴随切线。
为弦P1P2的伴随切线。
当a=2时,已知两点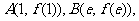 试求弦AB的伴随切线
试求弦AB的伴随切线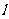 的方程;
的方程;
(III)设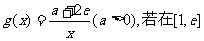 上至少存在一个
上至少存在一个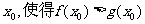 成立,求实数a的取值范围。
成立,求实数a的取值范围。
21.(本小题满分12分)
已知点P在椭圆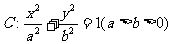 上,F1,F2分别为椭圆C的左、右焦点,满足|PF1|=6-|PF2|,且椭圆C的离心率为
上,F1,F2分别为椭圆C的左、右焦点,满足|PF1|=6-|PF2|,且椭圆C的离心率为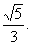
(I)求椭圆C的方程;
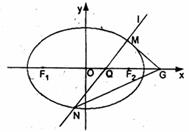
(II)若过点Q(1,0)且不与x轴垂直的直线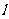 与椭圆C相交于两个不同点M、N,在x轴上是否存在定点G,使得
与椭圆C相交于两个不同点M、N,在x轴上是否存在定点G,使得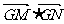 为定值,若存在,求出所有满足这种条件的点G的坐标;若不存在,说明理由。
为定值,若存在,求出所有满足这种条件的点G的坐标;若不存在,说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com