
6.若实数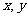 满足不等式
满足不等式 ,则
,则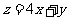 的最大值为
的最大值为
A.4 B.11 C.12 D.14
5.已知非零向量 和
和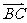 满足
满足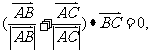 且
且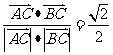 ,则△ABC为
,则△ABC为
A.等边三角形 B.等腰非直角三角形
C.非等腰三角形 D.等腰直角三角形
4.已知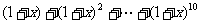 展开式中各项系数和为
展开式中各项系数和为
A.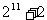 B.
B. C.
C.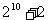 D.
D.
3.已知直线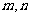 和平面
和平面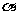 ,则
,则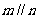 的一个必要非充分条件是
的一个必要非充分条件是
A.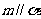 、
、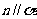 B.
B.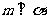 、
、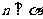
C.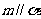 、
、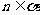 D.
D.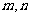 与
与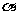 成等角
成等角
2.在等比数列 中,若
中,若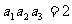 ,
,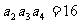 ,则公比
,则公比
A. B.
B.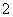 C.
C.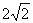 D.
D.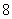
1.函数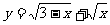 的定义域
的定义域
A.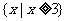 B.
B.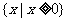 C.
C.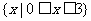 D.
D.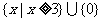
21.(本小题满分14分)
已知椭圆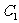 :
: 的左、右焦点分别为
的左、右焦点分别为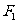 、
、 ,右顶点为
,右顶点为 ,
,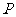 为椭圆
为椭圆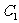 上任意一点,且
上任意一点,且 的最大值的取值范围是
的最大值的取值范围是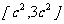 ,其中
,其中 .
.
(1)求椭圆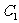 的离心率
的离心率 的取值范围;
的取值范围;
(2)设双曲线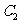 以
以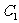 的焦点为顶点,顶点为焦点,
的焦点为顶点,顶点为焦点, 是双曲线
是双曲线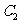 在第一象限内任意一点,当椭圆
在第一象限内任意一点,当椭圆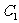 的离心率
的离心率 取最小值时,猜想是否存在常数
取最小值时,猜想是否存在常数 ,使得
,使得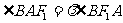 恒成立?若存在求出
恒成立?若存在求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
20.(本小题满分13分)
已知 ,且
,且 .
.
(1)求证:方程 总有两个正根;
总有两个正根;
(2)求不等式 的解集;
的解集;
(3)求使 对于
对于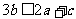 恒成立的
恒成立的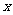 的取值范围.
的取值范围.
19.(本小题满分12分)
某工厂为解决职工的住房问题,计划在市郊征用一块土地,盖一幢总建筑面积为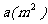 的宿舍楼,已知土地的征用费为
的宿舍楼,已知土地的征用费为 ,且每层的建筑面积相同,土地的征用面积为第一层的
,且每层的建筑面积相同,土地的征用面积为第一层的 倍.经工程技术人员核算,第一、二层的建筑费用相同,且都为
倍.经工程技术人员核算,第一、二层的建筑费用相同,且都为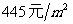 ,以后每层每增高一层,其建筑费用就增加
,以后每层每增高一层,其建筑费用就增加 .试设计这幢宿舍的楼高层数,使总费用最少,并求其最少费用(总费用为建筑费用与征地费用之和).
.试设计这幢宿舍的楼高层数,使总费用最少,并求其最少费用(总费用为建筑费用与征地费用之和).
18.(本小题满分12分)
如下图,正四棱柱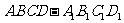 中,侧棱长为
中,侧棱长为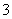 ,底面边长为
,底面边长为 ,
,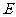 是棱
是棱 的中点.
的中点.
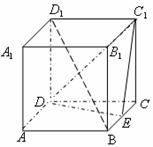
(1)求证: 平面
平面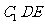 ;
;
(2)求二面角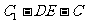 的大小;
的大小;
(3)在侧棱 上是否存在点
上是否存在点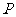 ,使得
,使得 平面
平面 ?证明你的结论
?证明你的结论
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com