
2.若将复数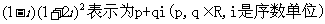 的形式,则p+q=
的形式,则p+q=
1.已知全集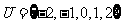 ,集合
,集合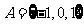 ,
,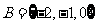 ,则
,则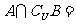
22.(本小题满分12分)
(理科)椭圆E的中心在坐标原点O,焦点在x轴上,离心率为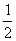 .点P(1,
.点P(1,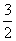 )、A、B在椭圆E上,且
)、A、B在椭圆E上,且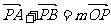 (m∈R).
(m∈R).
(Ⅰ)求椭圆E的方程及直线AB的斜率;
(Ⅱ)求证:当△PAB的面积取得最大值时,原点O是△PAB的重心.
(文科)椭圆E的中心在坐标原点O,焦点在x轴上,离心率为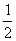 .点P(1,
.点P(1,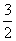 )、A、B在椭圆E上,且
)、A、B在椭圆E上,且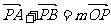 (m∈R).
(m∈R).
(Ⅰ)求椭圆E的方程;
(Ⅱ)当m=-3时,证明原点O是△PAB的重心,并求直线AB的方程.
|
21.(本小题满分12分)
已知数列{an}的前n项和为Sn,Sn=2-(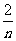 +1)an(n≥1).
+1)an(n≥1).
(Ⅰ)求证:数列{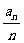 }是等比数列;
}是等比数列;
(Ⅱ)设数列{2nan}的前n项和为Tn,An=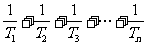 .
.
(理科)试比较An与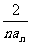 的大小
的大小
(文科)求证:An<2.
20.(本小题满分12分)
(理科)已知函数f(x)=eaxlnx在定义域内是增函数,求实数a的取值范围.
(文科)已知函数f(x)=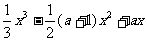 (a∈R).
(a∈R).
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若方程f(x)=0有三个不等实根,求a的取值范围.
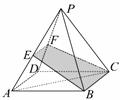
19.(本小题满分12分)
已知正四棱锥P-ABCD的底面边长为4,侧面与底面所成的二面角为60°,E、F分别是侧棱PA、PD的中点.求:
(Ⅰ)直线BE与侧棱PC所成的角的大小;
(Ⅱ)AC与截面BCFE所成的角的大小。
|
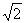 ,sinB-cosB=
,sinB-cosB=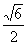 ,BC=2.
,BC=2.
(Ⅰ)求∠C;
(Ⅱ)求△ABC的面积.
18.(本小题满分12分)
有标号分别为1、2、3的三个电子元件,事件A、B、C分别表示“元件1损坏”、“元件2损坏”和“元件3损坏”(损坏的元件不再导电).事件D表示“电路两端有电流通过”.
(Ⅰ)分别就下列三种电路,用事件A、B、C(或其对立事件)表示事件D(每种电路只写出一种表示即可);

(Ⅱ)若元件1、2、3损坏的概率分别为0.1、0.2和0.3,求上面三种电路中,事件D发生的概率.根据计算推断,家用照明电路采用的是哪种联法?(假设每个元件的损坏与否是互不影响的)
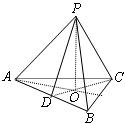
16.在正三棱锥P-ABC中,O是底面中心,PD是斜高(如图),小棱锥P-AOD中集中了正棱锥的许多重要元素,研究表明:在PO、PD、PA、OA、OD、AD、∠PDO、
∠PAO、∠PAD中,已知两个不全为角、也不全在底面AOD上的量,就可以求出其它各量。如果不考虑结论的变化,仅考虑两个已知条件的搭配情况,那么能编制_______种不同类型(如:已知PA、PD与已知PA、PO算作不同类型.用数字作答)的题目.
15.已知双曲线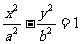 (a>0,b>0)的右焦点为F,过F且斜率为
(a>0,b>0)的右焦点为F,过F且斜率为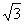 的直线l与右准线的交点P在该双曲线的渐近线上,则此双曲线的两条渐近线的夹角为_____.
的直线l与右准线的交点P在该双曲线的渐近线上,则此双曲线的两条渐近线的夹角为_____.
14.在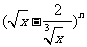 的展开式中,只有第5项的二项式系数最大,则展开式中含
的展开式中,只有第5项的二项式系数最大,则展开式中含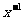 项为第_____项.
项为第_____项.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com