
20.(本小题共12分)、一种化工产品的单价随着其纯度的提高而提高,某化学公司计划要用单价为A元/千克的原料100千克进行提纯.每次提纯后产品的总价值按如下方法计算:每提纯一次,产品的重量将减少2%,随着产品纯度的提高,使提纯后产品的“初步单价”(即未扣除加工费时的“单价”)是提纯前单价的1.3倍,在此计算结果的基础上每提纯一次需要扣除的加工费用是本次提纯前总价值7.4%(注:本次提纯后的总价值=本次提纯后的重量×本次提纯后的单价).
(Ⅰ)问第一次提纯后产品的总价值是多少元?
(Ⅱ)求使这种产品总价值翻一番的最小提纯次数n的值(参考数据lg2=0.3010,lg3=0.4771.)
19.(本小题共12分)、数列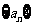 的前
的前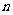 项和记为
项和记为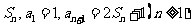
(Ⅰ)求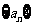 的通项公式;
的通项公式;
(Ⅱ)等差数列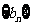 的各项为正,其前
的各项为正,其前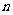 项和为
项和为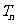 ,且
,且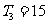 ,又
,又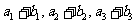 成等比数列,求
成等比数列,求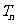
18.(本题12分)如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,
且PA=AB=2,E是PB的中点,F是AD的中点.
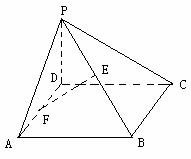
(Ⅰ)求异面直线PD与AE所成角的大小;
(Ⅱ)求证:EF⊥平面PBC.;
(Ⅲ)求二面角F-PC-B的大小.
17.(本题10分)已知函数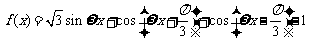 (
( ,
,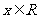 ),且函数
),且函数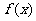 的最小正周期为
的最小正周期为 .
.
(Ⅰ)求函数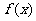 的解析式并求
的解析式并求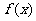 的最小值;
的最小值;
(Ⅱ)在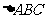 中,角A,B,C所对的边分别为
中,角A,B,C所对的边分别为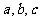 ,若
,若 =1,
=1,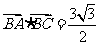 ,
,
且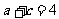 ,求边长
,求边长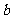 .
.
16.已知 为常数,函数
为常数,函数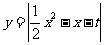 在区间
在区间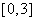 上的最大值为2,则
上的最大值为2,则
15.从平行六面体的8个顶点中任取5个顶点为顶点,恰好构成四棱锥的概率为________
14.设双曲线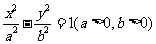 的右焦点为
的右焦点为 ,右准线
,右准线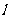 与两条渐近线交于P、
与两条渐近线交于P、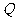 两点,如果
两点,如果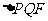 是直角三角形,则双曲线的离心率
是直角三角形,则双曲线的离心率 .
.
13.若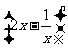 展开式的二项式系数之和为64,则其展开式中的常数项为___________
展开式的二项式系数之和为64,则其展开式中的常数项为___________
12.已知正三棱柱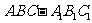 的底面边长为2,高为1,过顶点A作一平面
的底面边长为2,高为1,过顶点A作一平面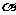 与侧面
与侧面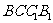 交于
交于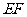 ,且
,且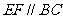 .若平面
.若平面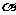 与底面
与底面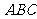 所成二面角的大小为
所成二面角的大小为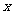
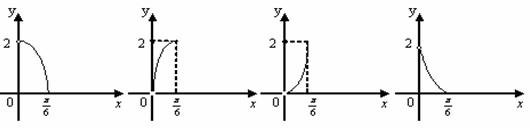
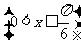 ,四边形
,四边形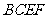 面积为y ,则函数
面积为y ,则函数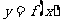 的图象大致是
的图象大致是
A B C D
第Ⅱ卷(非选择题)
11.棱长为1的正方体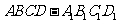 的8个顶点都在球
的8个顶点都在球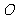 的表面上,E,F分别为棱AB,A1D1的中点,则经过E,F球的截面面积的最小值为
的表面上,E,F分别为棱AB,A1D1的中点,则经过E,F球的截面面积的最小值为
A. 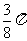 B.
B. 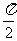 C.
C.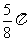 D.
D.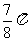
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com